Question: Topology for Question 4 is defined by the answer for Question 2 (a). Sorry for the mess. 4. Prove a version of the
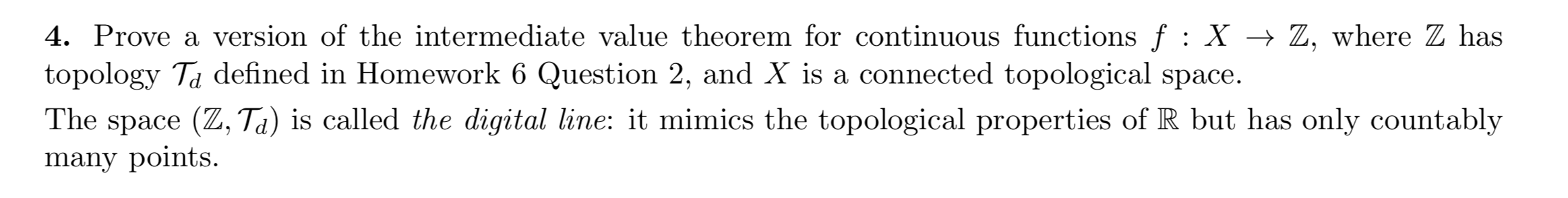

Topology "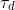 " for Question 4 is defined by the answer for Question 2 (a). Sorry for the mess.
" for Question 4 is defined by the answer for Question 2 (a). Sorry for the mess.
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


