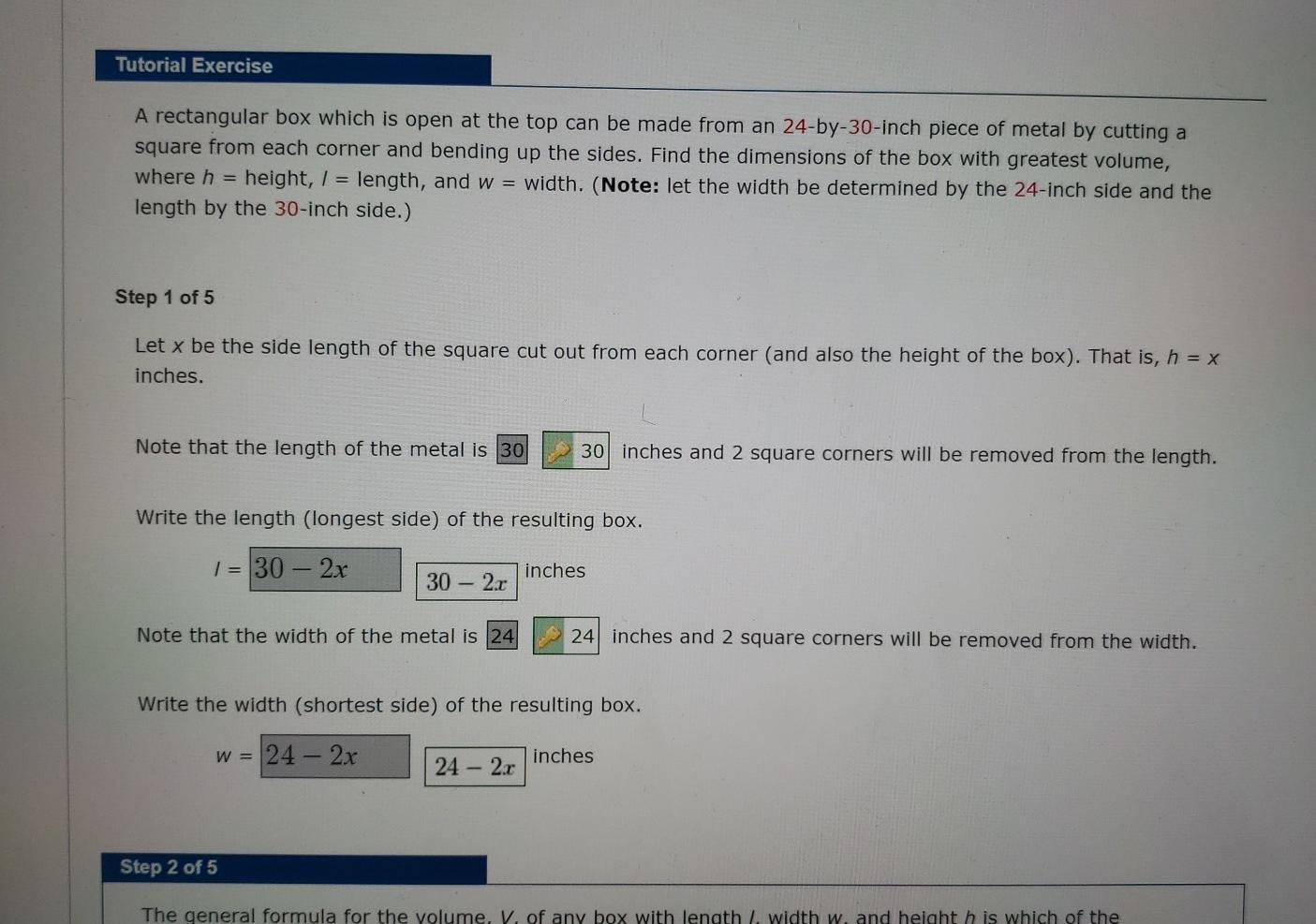
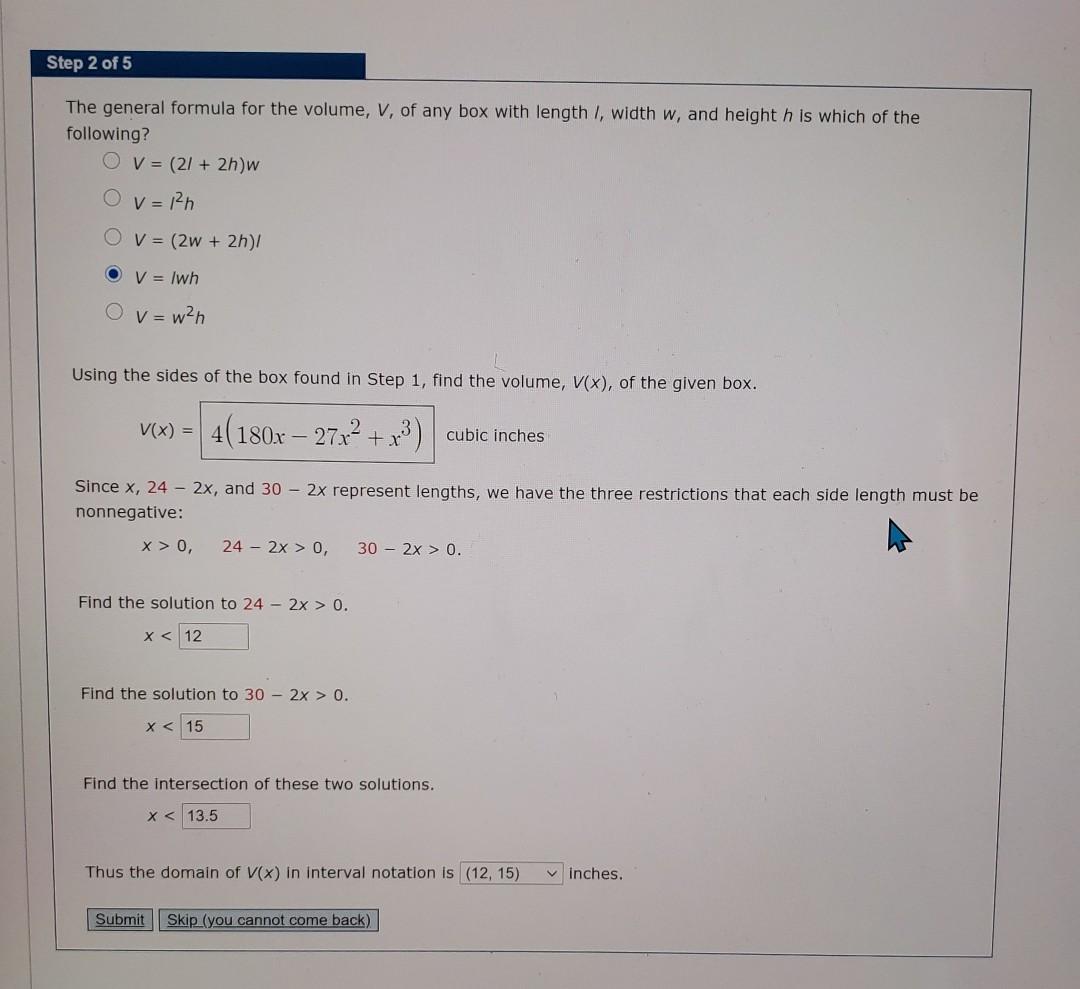
Tutorial Exercise A rectangular box which is open at the top can be made from an 24-by-30-inch piece of metal by cutting a square from each corner and bending up the sides. Find the dimensions of the box with greatest volume, where h = height, /= length, and w = width. (Note: let the width be determined by the 24-inch side and the length by the 30-inch side.) Step 1 of 5 Let x be the side length of the square cut out from each corner (and also the height of the box). That is, h = x inches. Note that the length of the metal is 30 Write the length (longest side) of the resulting box. /= 30 - 2x 30 - 2x Note that the width of the metal is 24 30 inches and 2 square corners will be removed from the length. 24 - 2x inches 24 inches and 2 square corners will be removed from the width. Write the width (shortest side) of the resulting box. w = 24-2x inches Step 2 of 5 The general formula for the volume. V. of any box with length /. width w. and height h is which of the Step 2 of 5 The general formula for the volume, V, of any box with length /, width w, and height h is which of the following? OV= (21+ 2h)w V = 1h V = (2W + 2h)/ V = /wh V = wh O O Using the sides of the box found in Step 1, find the volume, V(x), of the given box. V(x) = 4(180x27x + x) cubic inches Since x, 24 - 2x, and 30- 2x represent lengths, we have the three restrictions that each side length must be nonnegative: x > 0, 24 - 2x > 0, 30 - 2x > 0. Find the solution to 24 - 2x > 0. x < 12 Find the solution to 30 - 2x > 0. x < 15 Find the intersection of these two solutions. x < 13.5 Thus the domain of V(x) in interval notation is (12, 15) Submit Skip (you cannot come back) inches.