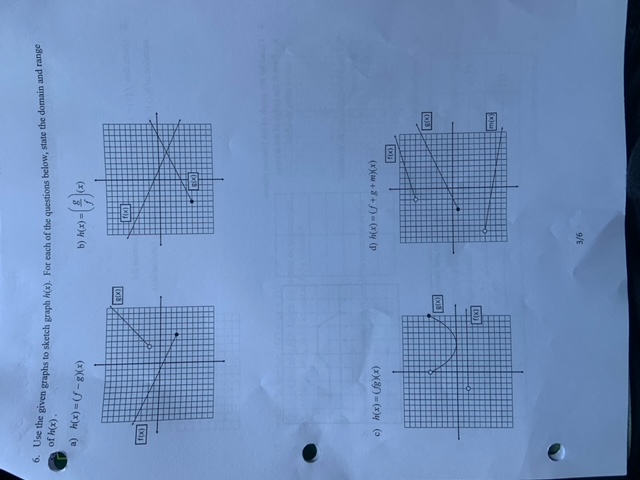
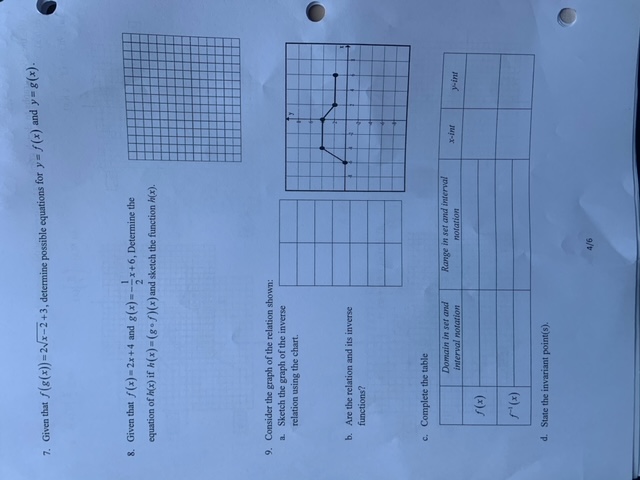
Two functions, f(x) and g (x) are given as following. f (x)= x +2, where D=(x]-25x 52,xe R) g(x) = x, where D = (x |-2 5 x$ 2, xe R) Answer the following questions. 1. The value of (P(-2 ) - ((-2 ) . (f-g)(-2) is_(Place answer in the first box.)(-2) +2)-(2) . (fog) (2) is 4+240 ) = 8 (Place answer in the second box. 2. The value of . (f-g) (0) is . (Place answer in the first box.) (4 (2) is . (Place answer in the second box.) 3. The range of (fog) (x) can be written in the form (oasysb, ve R), where a, be N . The value of a is .(Place answer in the first box.) b is (Place answer in the second box.) 4. The range of (f - g) (x) can be written in the form (Macysb. ye R), where a, be N . The value of . a is (Place answer in the first box.) bis (Place answer in the second box.) 1/6\f\f7. Given that / (g(x)) = 2w/x-2 +3, determine possible equations for y = / (x) and y = g(x). 8. Given that / (x) = 2x +4 and g(x)= -- x+6, Determine the equation of Mx) if h(x) = (go f)(x) and sketch the function h(x). 9. Consider the graph of the relation shown: a. Sketch the graph of the inverse relation using the chart. b. Are the relation and it's inverse functions? C. Complete the table Domain in set and Range in set and interval interval notation Horation f (x) d. State the invariant point(s).10. For the two given functions, /(x)=- and g(x)= vx-6, determine the domain of the following composite functions. a) fof b) fog 11. Consider the function f(x) = (x + 2)3 a. Graph the function /{x). Graph the inverse on the same set of coordinate axes. Is the inverse of /(x) a function? 10 8 6 4 2 6 8 10 b. Describe how the domain of /(x) could be restricted so that the inverse of f(x) is a function. 12. Which of these functions need to have their domains restricted in order to define and inverse? For those functions, how would you restrict their domains? a) /(x)=x+2x+1 b) /(x)=x c) /(x) =5-x 5/6\f