UPDATED

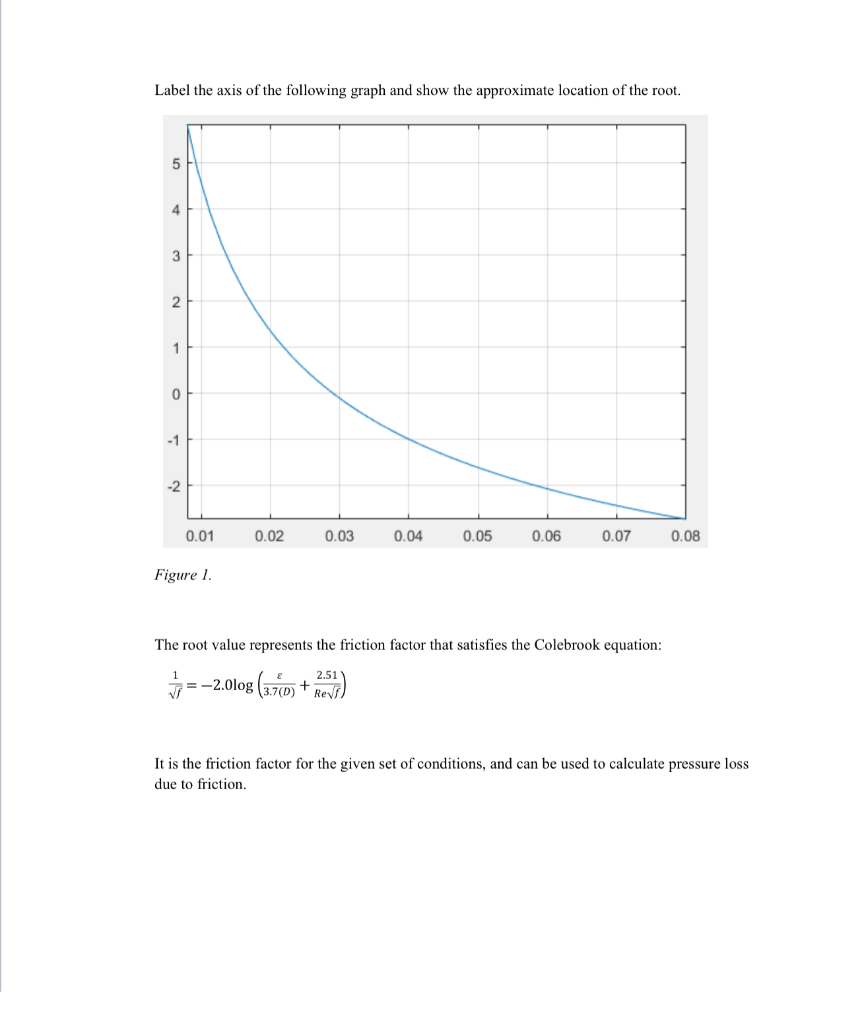
Please copy and paste your MATLAB code it would be very appreciated. I am so stuck.

Complete Problem 2 with MATLAB. Submit your script, any appropriate figures, and answers to the questions. 2. As an engineer, designing a cooling system, you are responsible for quantifying the friction factor, f, for air flowing through a smooth, thin tube. The friction factor is a dimensionless parameter used for quantifying pressure loss (along with other parameters), in some cases it can be obtained by iteratively solving the Colebrook equation. Implement the Newton-Raphson method to approximate the friction factor using the Colebrook equation. Answer the questions that conclude this problem. Properties: Fluid's Density: Dynamics Viscosity: Tube Diameter: Velocity: Roughness: Reynolds Number: p= 1.233 u = 1.79. 10-5N :$/m2 D=0.005 m V = 40"/ E = 0.0015 mm Re = 13743 (Ratio of inertial forces to viscous forces) The Colebrook equation: =-20log (3,760 + R. ) After substituting numerical values for the variables, the Colebrook equation is as follows (verify there is consistency with units): Rearrange the Colebrook equation to have a function of the unknown variable: Label the axis of the following graph and show the approximate location of the root. 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 Figure 1. The root value represents the friction factor that satisfies the Colebrook equation: =-2.0log (3.10) + R) It is the friction factor for the given set of conditions, and can be used to calculate pressure loss due to friction. Complete six iterations and calculate the absolute relative approximate percent error after each iteration. Construct a table to store your values. Initial Guess: Xo = 0.008 i L x, Xit Teal % O 0.008 Table 1: Initial Guess of 0.008 Now, compute six iterations using a different initial guess of 0.08. Store the values in the Table 2. Initial Guess: Xo = 0.08 X L Xit Teal % 0 0.08 Table 2: Initial Guess of 0.08 Answer the following questions 1) In this case study what is being solved? 2) What does the solution represent? 3) Compare the results from Tables land 2. Why is there is difference when the initial guess changes? What can be inferred from the results presented in Tables 1 and 2