1. Use a graphing calculator or technology to perform sinusoidal regression that will determine the sine function that best fits the data. Record the equation.
2. Choose a temperature (not a max or min temperature) and use the equation from part a) to find the months when the temperature is above your chosen temperature.
3. Choose a month when the temperature is changing at a negative rate. Determine the instantaneous rate of change of temperature at that point.

SAMPLE:

• All sunrise and sunset data are taken from the first day of each month.
• All times have been converted to hours using decimal values: i.e. 5 hr 45 min = 5 + 45/60 = 5.75 hrs.
• Daylight hours are the difference between sunset time and sunrise time.
• Temperature is the average monthly temperature.
• DATA:

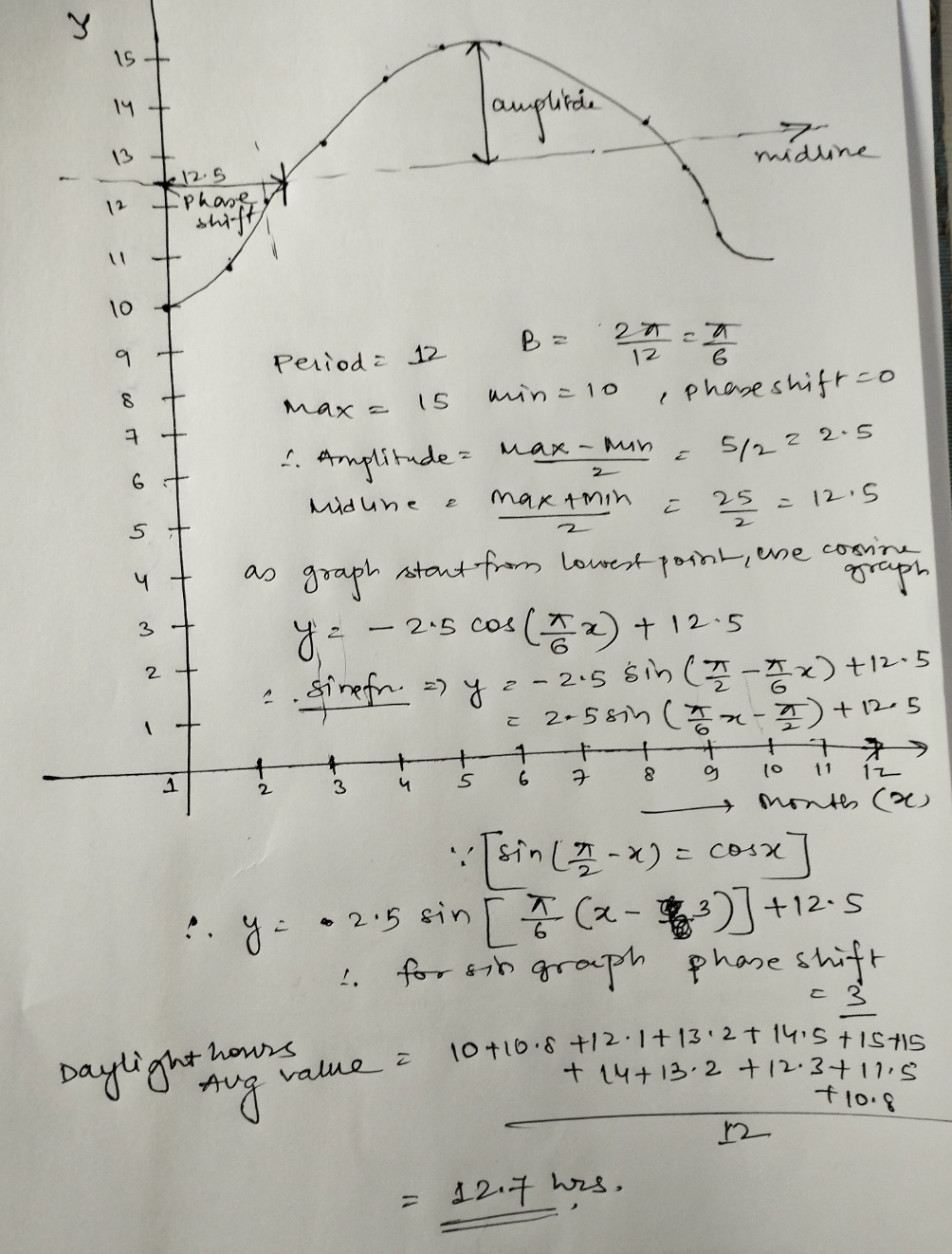
15 19 amplifi. 13 -12 . 5 midline 12 phase, shift 11 10 9 Period= 12 B = 21 = 12 8 6 Max = 15 win = 10 Iphoneshift so 7 6 ". Amplitude = Max - Min - 5/2 2 2. 5 5 Midline = martmin = 25 = 1215 as graph start from lowest point, we cosine graph 3 42 - 215 COS ( A x ) + 12.5 2 :. sinefn ?) 4 2 - 2.5 8in ( 7 - X x ) + 12. 5 = 2 + 5 8in ( II Ex - I ) + 12. 5 N - 3 u + 8 10 11 12 month (2) . : sin ( I - x ) = cosx ] .. y = $2 .5 sin [ ( x -$3)]+ 12.5 1. for sin graph phase shift Daylight hours Avg value 2 10 + 10 . 8 + 12 . 1+ 13 : 2 + 1415 + 15+15 + 14 + 13 . 2 + 12. 3+ 11,5 + 10. 8 12 = 12 7 was