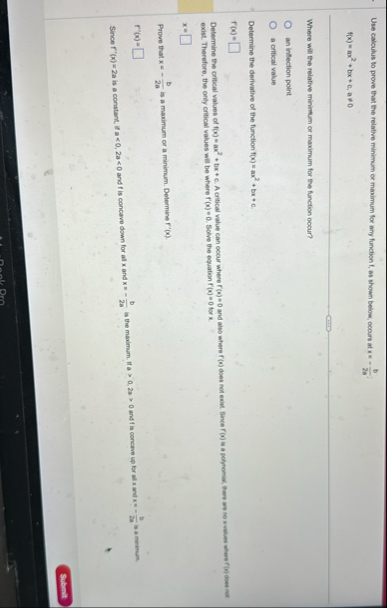
Use calculus to prove that the relative minimum or maximum for ary function f $,$ as shown below, occurs at $x=-\frac{b}{2a}.$

$f(x)=a{x}^{2}bxc,a0$

Where will the relative minimum or maximum for the function occur?

an infection point

a critical value

Determine the derivative of the function $f(x)=a{x}^{2}bxc.$

$r(x)=$

$$ exist. Therefore, the only critical values will be where $f^{\text{'}}(x)=0.$ Solve the equation $f^{\text{'}}(x)=0$ for $x.$

$x=$

$$

Prove that $x=-\frac{b}{2a}$ is a maximum or a minimum. Determine $f^{\text{'}}(x).$

$r^{\text{'}\text{'}}(x)=$

$$ Since $f^{\text{'}}(x)=2a$ is a constant, if and f is concave down for all x and $x=-\frac{b}{2a}$ is the maximum. if $a>0,2a>0$ and f is concave up for all x and $x=-\frac{b}{2a}$ is a minum.