Use data below to answer

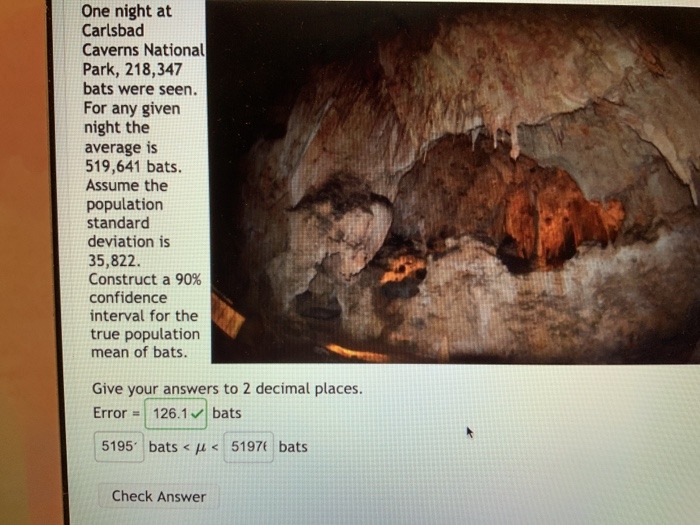
One night at Carlsbad Caverns National Park, 218,347 bats were seen. For any given night the average is 519,641 bats. Assume the population standard deviation is 35,822. Construct a 90% confidence interval for the true population mean of bats. Give your answers to 2 decimal places. Error = 126.1 bats 5195 bats 0. 12. The test statistic is 0.91, the p-value is 0.18. B Ho: Pas = 0. 12 vs Ha: Pas > 0. 12. The test statistic is 0.97, the p-value is 0.17. C) Ho: Pas = 0. 12 vs Ha: Pas > 0. 12. The test statistic is 2.44, the p-value is 0.007. D Ho : Pas = 0. 12. vs Ha: Pas # 0. 12. The test statistic is 0.91, the p-value is 0.18. E Ho: Pas = 0. 12 vs Ha : pas # 0. 12. The test statistic is 2.44, the p-value is 0.007.Use the following to answer questions 33 - 38. Here a two-way table of those aboard the Titanic, classified according to the class of ticket person survived or did not survive the crash. Class Survival status Totals First Second Third Crew 118 178 212 711 * Survived 203 1490 Did not survive 127 167 528 673 285 385 2201 Totals 325 706 33. Find the probability that a randomly selected person aboard the Titanic survived the crash, given that he/she was a crew member. (A) 0.8034 (B) 0.2982 (C) 0.0963 (D) 0.2395 (E) None of these 34. Find the probability that a randomly selected person aboard the Titanic either survived the crash or had the First-Class ticket. (A) 0,423 (B) 0.4707 (C) 0.3785 (D) 0. 0922 (E) None of these 35. Find the percent First-Class ticket holders aboard the Titanic that did not survive the crash. (A] 8.19% (B) 37.54% (C)5.54% (D) 14.77% (E) None of these 36. Classify the following events "selected person aboard the Titanic has a Second-Class ticket" and "selected person aboard the Titanic survived the crash" as: (A) Complementary (B) Not complementary 37. Classify the following events "selected person aboard the Titanic has a Second-Class ticket" and "selected person aboard the Titanic survived the crash" as: (A) Disjoint (mutually exclusive] (8) Not disjoint (not mutually exclusive) 38. We are interested to determine whether "selected person aboard the Titanic has a Second-Class ticket" and "selected person aboard the Titanic survived the crash" are independent or dependent events. To answer this question, we start by finding P (Second-Class]. With what probability it makes sense to compare P/Second-Class] in order to answer the question about independence? (A) P [Survived) (B) P (Second-Class | Survived) (C) P (Survived | Second-Class) (D) P (Survived and Second-Class) (E) None of these 39. Assuming Z is the standard normal distribution, find P (Z 2-1.35). (A) 0.0885 (B) 0.9115 (C) 0.5895 (D) 0.4115 (E) None of these