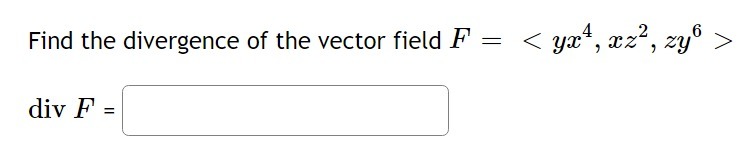
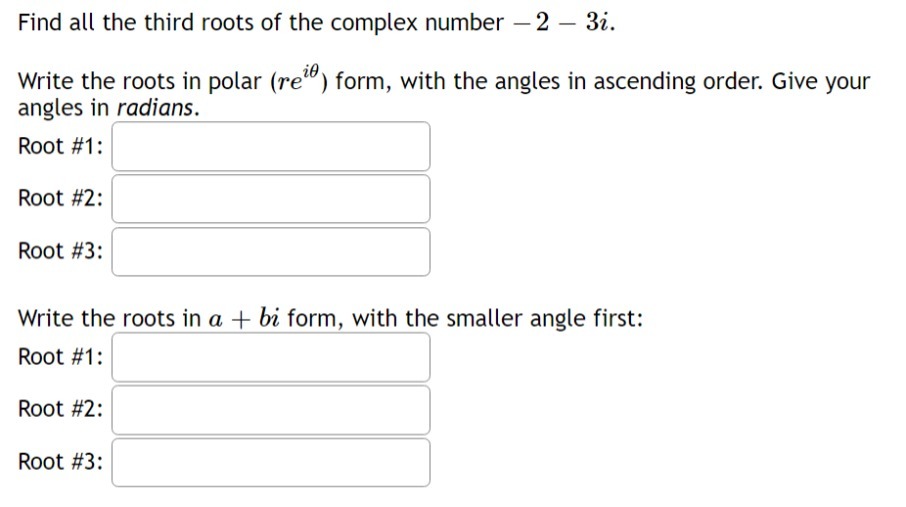
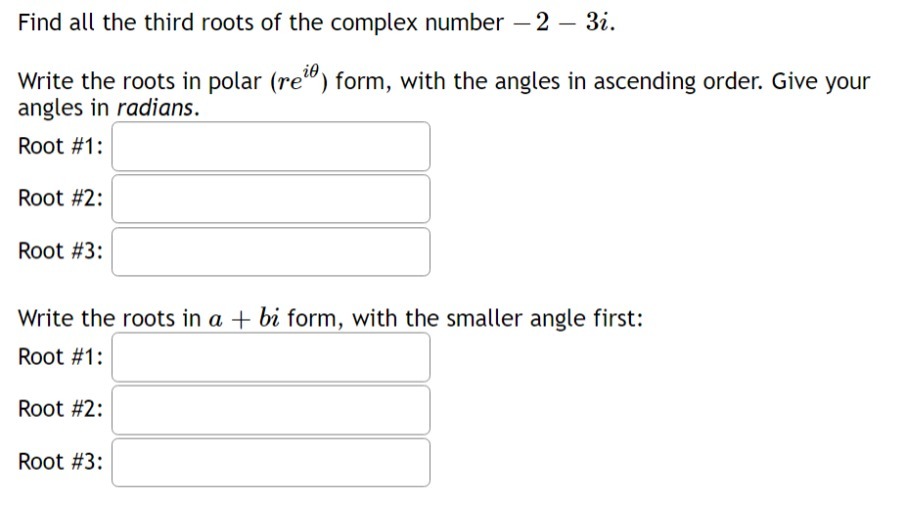
Use Green's Theorem to evaluate: F . n ds C where F = ( va + 3y, 2x + 3y) and C is the boundary of the region enclosed by y = 4x - x- and the -axis (oriented positively).The general solution to this ODE: is: Use (:1 and oz for any undetermined constants in your solution. Find the divergence of the vector field F = div F =Find all the third roots of the complex number 2 33?. Write the roots in polar (raw) form, with the angles in ascending order. Give your angles in radians. Root #1: ' I Root #2: ' I Write the roots in a + bi form, with the smaller angle first: Root #1: ' l Root #2: I ] Root #3: ' I Find the curl of the vector field F = curl F = kIf {x, y, z, w} is a linearly independent set in R", which of the following sets is linearly independent? C] {xy,yz,zw,wx} {x+y,y+z,z+x} C] {xy,yz,zx} D{x+y,y+z,z+w,w+x} Convert the complex number to polar form. -2 - 2V3i Give your answer in r( cos + 2 sin form.