Question: Use MATLAB to implement theorom. Please show output function y = hermite(X,Y,YP, x) %start at x 1 instead of x 0 % % % X=[1.0
Use MATLAB to implement theorom. Please show output

function y = hermite(X,Y,YP, x)
%start at x1 instead of x0
%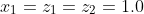
%![3.0] % % % Y=[1.10517 1.49182 2.45960] % % % YP=[0.22103 0.59673](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/09/66f2e5956d7b7_51566f2e593dd5d6.jpg)
%![1.47576] %Iterpolation point x=1.25 %when outputted should output y = 1.1690 Example](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/09/66f2e595f01ae_51766f2e59599f42.jpg)
X=[1.0 2.0 3.0]
%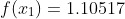
%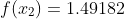
%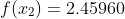
Y=[1.10517 1.49182 2.45960]
%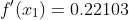
%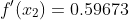
%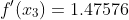
YP=[0.22103 0.59673 1.47576]
%Iterpolation point
x=1.25
%when outputted should output y = 1.1690

Example

Should formulate Hermite polynomial and plug in x=1.25 to get y=1.1690
Example
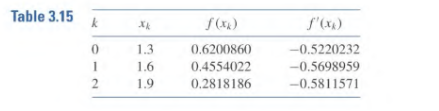

Thank you!
Write a MATLAB function to implement the Hermite interpolation in Algorithm 3.3. Note that the index should run from 1 instead of 0 that is used in the textbook. This is because MATLAB does not allow index0. Your function should use the same order of input below. Note that we do not return Q as in the algorithm. Instead, we calculate the interpolated function value at x. function y = hermite (X, Y, YF,x) X-numbers x 1 x 2 x n Y= values f (x 1) f(x 2) f(x n) YP-values f, (x1) f, (x2) f, (xn) x = interpolation point x - - % y-interpolated function value at x, i.e. H(x) your implementation below end Save your function in hermite.m', and interpolate the tabular function given below at the point x 1.25. f(x) f (a) 10517 0.22103 0.59673 2.45960 147576 Your function should return 11690. r3 253.0 f(x) 1.105 17 f(M) = 2.45960 f'(x2) = 0.59673 Hermite Interpolation To obtain the coefficients of the Hermite interpolating polynomial H(x) on the (n 3.3 I) distinct numbersxo.. n for the function f: INPUT numbers Xo, . . . . . xni values f(xo), . . . , f(x") and f'(h), . . ., f,(%). OUTPUTthe numbers Qo.o.Q1.1.... Q2n+1.2n+1 where 02+1.24x xo)x -x)x -x-(x -xn). Step 1 For i = 0. I.. , . , n do Steps 2 and 3 Step 2 Setz2i=Xi; Q2i.o = f(xi); Qu+1.0= f(xi); Step 3 If i 0 then set i22i- Step 4 For i 2,3,.. 2n1 for j = 2, 3, set Qi.j = Step 5 OUTPUT (Qo.o.1. .Q2n+.2+1 STOP Table 3.15 k S(x) 0.5220232 f(xx) 0 1.3 0.6200860 1.6 045540220.5698959 2 .9 0.2818186 0.5811571 Example 2 Use the data given in Example 1 and the divided difference method to determine the Hermite polynomial approximation at 1.5. Solution The underlined entries in the first three columns of Table 3.17 are the data given in Example 1. The remaining entries in this table are generated by the standard divided- difference formula (3.9) For example, for the second entry in the third column we use the second 1.3 entry in the second column and the first 1.6 entry in that column to obtain 0.4554022-0.6200860 1.6-1.3 =-0.5489460. For the first entry in the fourth column, we use the first 1.3 entry in the third column and the first 1.6 entry in that column to obtain -0.5489460 (-0.5220232) 1.6-1.3 -0.0897427 The value of the Hermite polynomial at 1.5 is Hs(1.5)-I3+31.5- 1.3)+FI1.3, 1.3, 1.6(1.5-1.3) +1.3, 1.3, 1.6, 1.61.5-1.3) (1.5 16) +fI1.3, 1.3, 1.6, 1.6, 1.9101.5-1.3)(1.5-1.6 +f11.3, 1.3, 6,6, 1.9, 1.9101.5-1.35 .61.5-1.9) 0.6200860-0.5220232)(0.2)-0.0897427)(0.2) 0.0663657(0.2)2-0.1)+0.0026663(0.2)2-0.1)2 (-0.0027738)(0.2)2-0.1)(-0.4) 0.5118277
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


