Use the formula to solve the question. I just need help with 1) and 2)

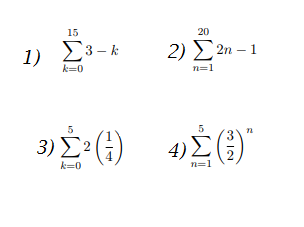
Equation 9.2. Sums of Arithmetic and Geometric Sequence-r - TheaumSoftherstntermaofanarithmeticaequenceek=c+{ir1)darlrzlis While we have made an honest effort to derive the formulas in Equation 9.2, formal proofs require the machinery in Section 9.3. An application of the arithmetic sum formula which proves useful in lCalculus results in formula for the sum of the rst n natural numbers. The natural numbers themselves are a sequence{1 1, 2, 3, . .. which is arithmetic with o = d = 1. Applying Equation 9.2, n{n+ 1] 2 So, for example, the sum of the rst 1m natural numbers5 is 1au21c1 = . An important application of the geometric sum formula is the investment plan called an annuity. Annuities differ from the lrind of invmtments we studied in Section .5 in that payments are deposited into the account on an on-going basis, and this complicates the mathematics a little. Suppose you have an account with annual interest rate 1* which is compounded n times per year. We let 1' = % denote the interest rate per period. Suppose we wish to malre ongoing deposits of P dollars at the end of each compounding period. Let A], denote the amount in the account after i: compounding periods. Then A, = P, because we have made our rst deposit at the end of the rst compounding period and no interest has been earned. During the second compounding period, we earn interest on A, so that our initial investment has grown to Al + i} = Pf] + i} in accordance with Equation 651. When we add our second payment at the end of the second period, we get 1+2+3+...+ = 1 A:=Ar[l+i]l+P=P{1+i}+P=P{l+i] (14-144) The reason for factoring out the PH + i] will become apparent in short order. During the third compounding period, we earn interest on A: which then grows to Ag] + i}. We add our third \f