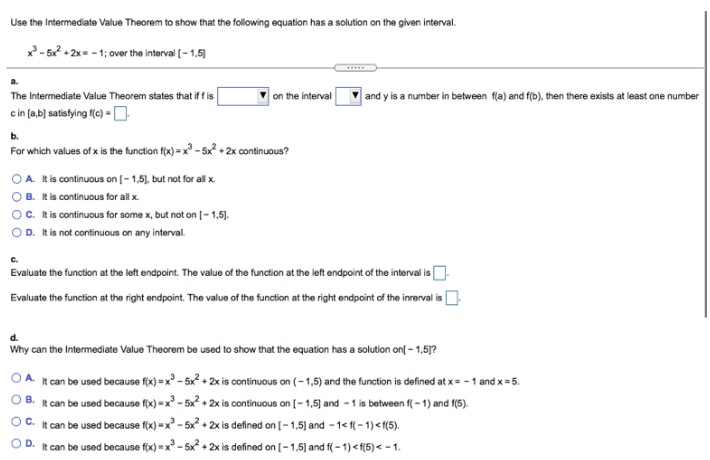
Use the Intermediate Value Theorem to show that the following equation has a solution on the given interval. x3 - 5x3+2x = - 1; over the interval [ - 1,5] a. The Intermediate Value Theorem states that if f is on the interval and y is a number in between fla) and f(b), then there exists at least one number c in [a,b] satisfying (c) =] b. For which values of x is the function ((x) = x -5x +2x continuous? O A. It is continuous on [- 1,5], but not for all x. O B. It is continuous for all x. O C. It is continuous for some x, but not on [ = 1,5]. O D. It is not continuous on any interval C. Evaluate the function at the left endpoint. The value of the function at the left endpoint of the interval is]. Evaluate the function at the right endpoint. The value of the function at the right endpoint of the interval is]. d. Why can the Intermediate Value Theorem be used to show that the equation has a solution on[ - 1,517 A. It can be used because fix) =x - 5x-+ 2x is continuous on (- 1,5) and the function is defined at x = - 1 and x = 5. O B. It can be used because fix) =x"- 5x7+ 2x is continuous on [- 1,5] and - 1 is between f( - 1) and 1(5). O G. It can be used because fix) =x3- 5x7+ 2x is defined on [- 1.5] and - 1