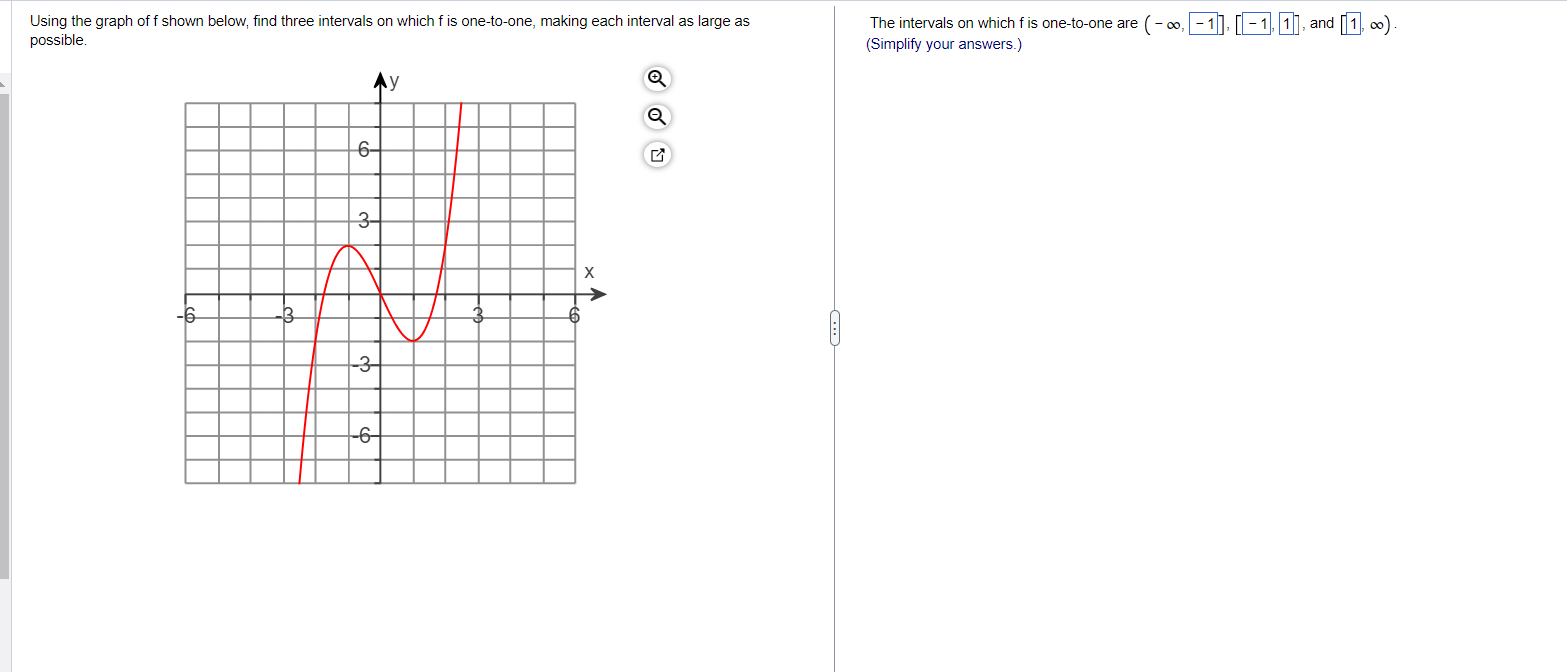
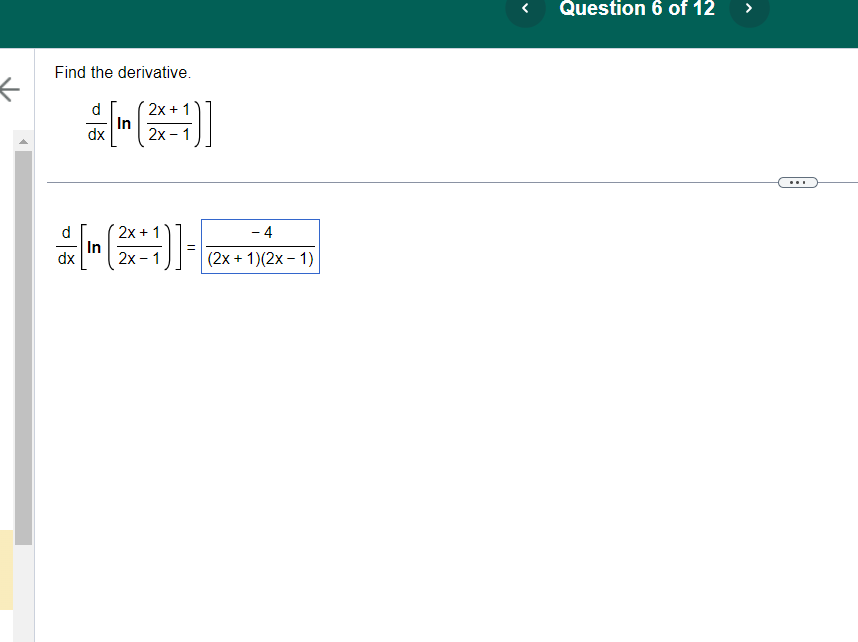
Using the graph of f shown below, find three intervals on which f is one-to-one, making each interval as large as The intervals on which f is one-to-one are ( -0, -1 '|, [ -1\\ 1 ", and [E, possible (Simplify your answers ) This question: 1 point(s) possible a. Use the Intermediate Value Theorem to show that the following equation has a solution on the given interval. b. Use the graphing utility to find all the solutions to the equation on the given interval. c. Illustrate your answers with an appropriate graph. (x* + 17x3 +7 =4; (0,1) a. The Intermediate Value Theorem states that if fis continuous on the interval [a,b] and L is a number strictly between f(a) and f(b), then there exists at least one number c in (a,b) satisfying f(c) = L. For which value(s) of x is the function f(x) = vx* + 17x +7 continuous? O A. It is continuous for all x. O B. It is continuous on [0, 1], but not for all x. O C. It is continuous for some x, but not on [0, 1]. O D. It is not continuous on any interval. Evaluate the function at the left endpoint. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. The value of the function at the left endpoint is 2.646. (Type an integer or decimal rounded to three decimal places as needed.) O B. The value of the function at the left endpoint is undefined. Evaluate the function at the right endpoint. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. The value of the function at the right endpoint is 5 Type an integer or decimal rounded to three decimal places as needed.) O B. The value of the function at the right endpoint is undefined. Why can the Intermediate Value Theorem be used to show that the equation has a solution on (0,1)? JA. It can be used because (x" + 17x" +7 is continuous on [0, 1] and the function is defined at x = 0 and x = 1. B. It can be used because (x" + 17x" +7 is defined on (0, 1) and 4 is greater than the values of the function at the two endpoints. C. It can be used because vx" + 17x" +7 is defined on (0, 1) and 4 is less than the values of the function at the two endpoints. D. It can be used because vx" + 17x" +7 is continuous on [0, 1] and 4 lies between the values of the function at the two endpoints. b. There is a solution to the equation on (0, 1) at x 4. (Round to the nearest thousandth as needed.)\f