use this to answer multiple choice questions!^

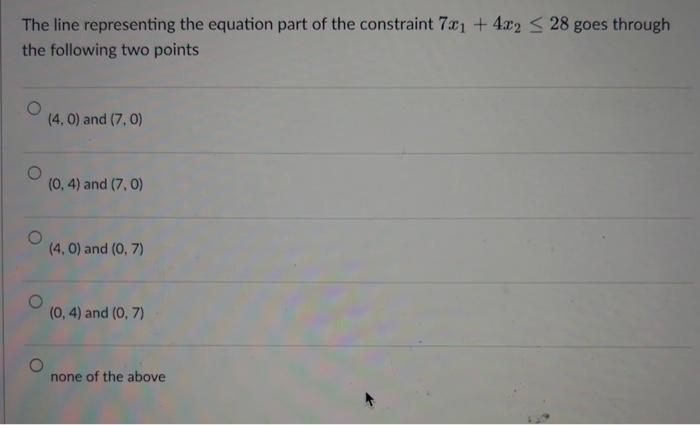
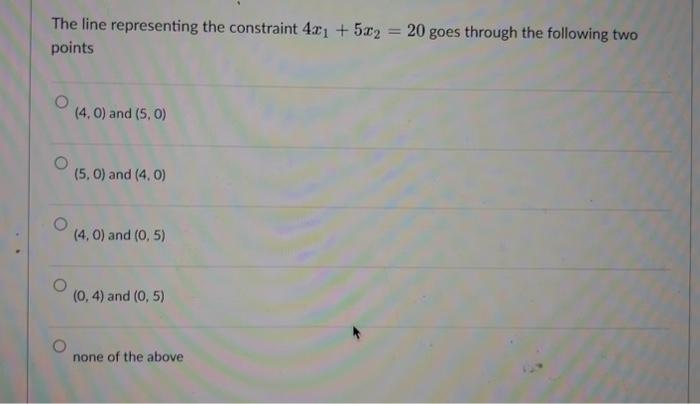
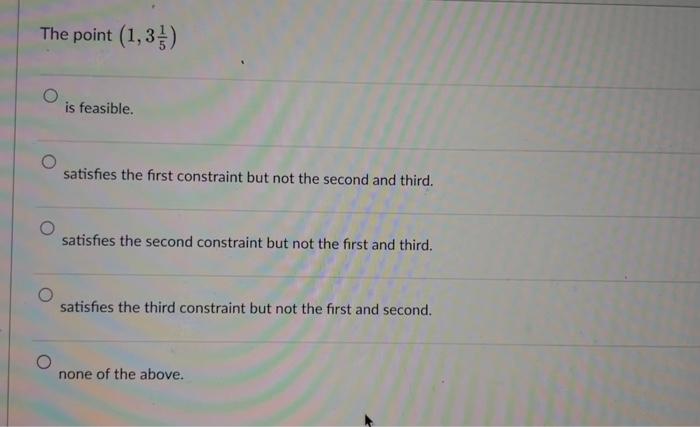
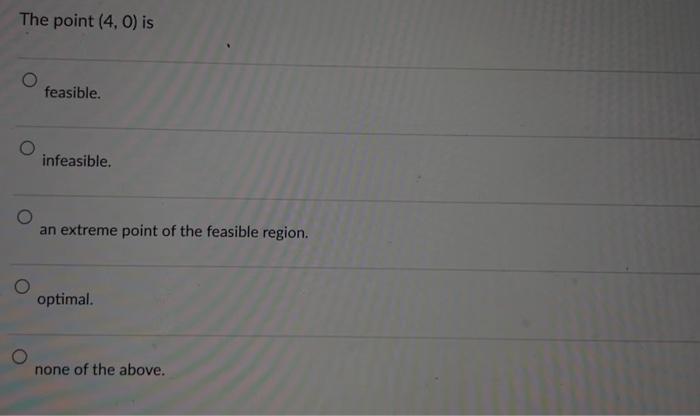
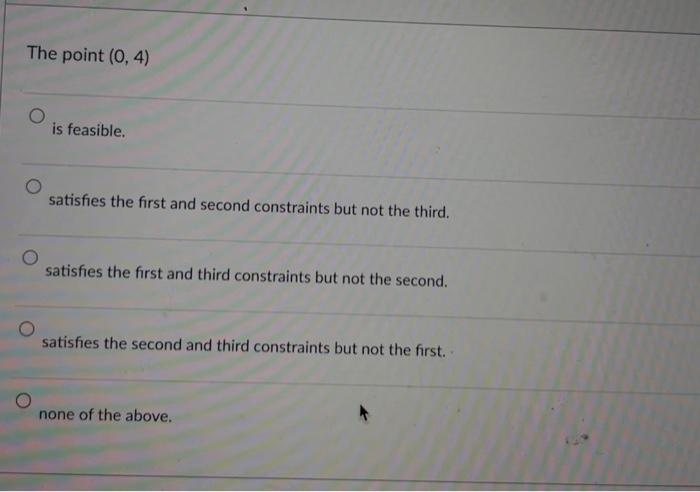
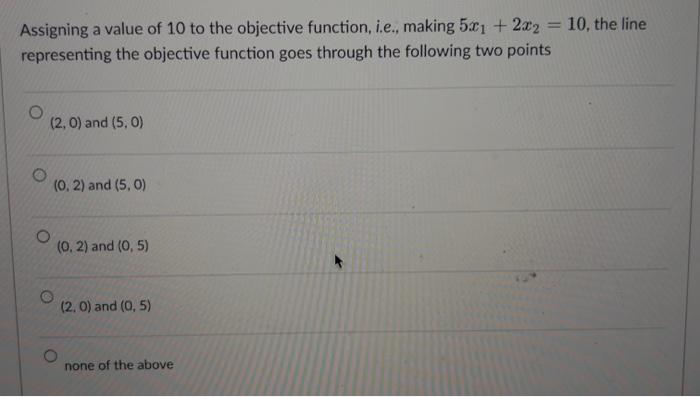
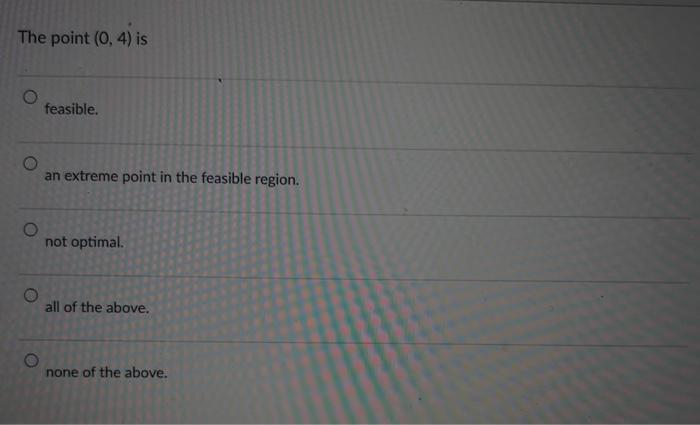
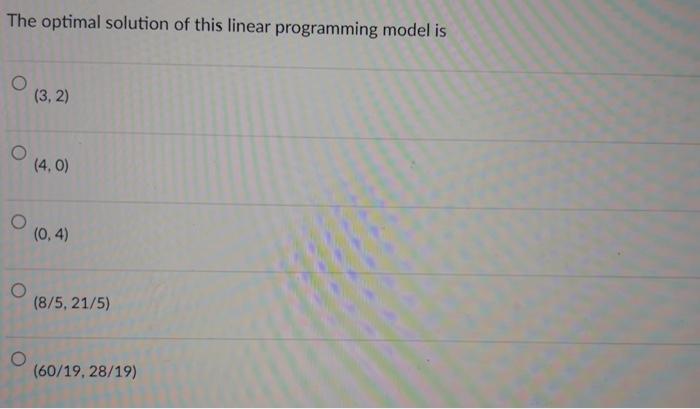
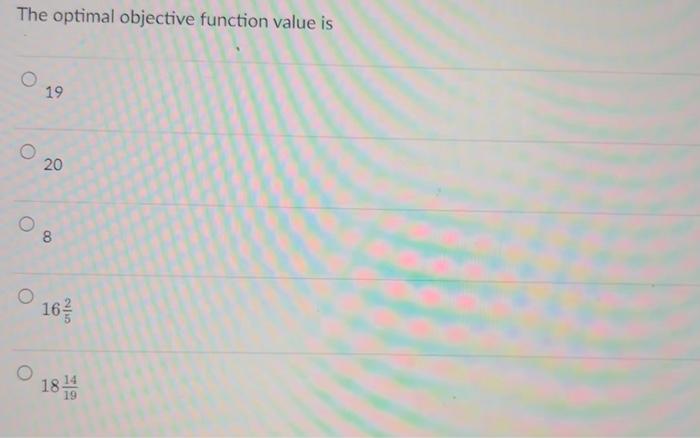
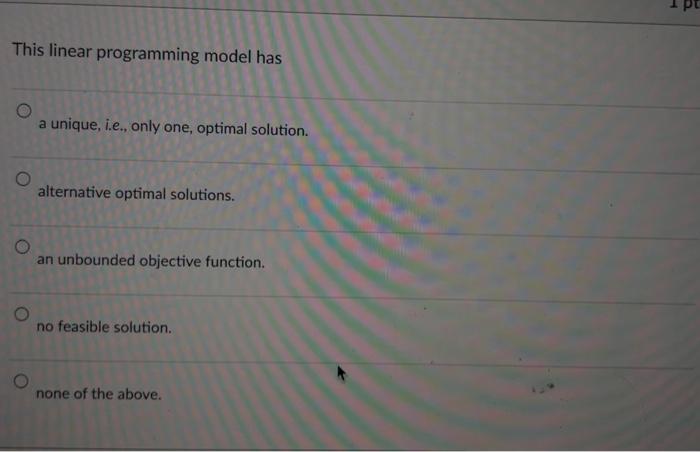
The point (4,0) is feasible. infeasible. an extreme point of the feasible region. optimal. none of the above. Solve the following linear programming problem with the graphic methods. Label the line for each of the constraints and shade the feasible region. Draw at least one line for the objective function. Indicate the optimal solution on the graph. Find the values of x1 and x2 as well as the value of the objective function, at the optimal solution. Maxs.t5x1+2x27x1+4x2281x1+2x2104x1+5x2=20 x1,x20 The line representing the equation part of the constraint 7x1+4x228 goes through the following two points (4,0) and (7,0) (0,4) and (7,0) (4,0) and (0,7) (0,4) and (0,7) none of the above The optimal objective function value is 19 20 8 1652 181914 This linear programming model has a unique, i.e., only one, optimal solution. alternative optimal solutions. an unbounded objective function. no feasible solution. none of the above. The point (0,4) is feasible. an extreme point in the feasible region. not optimal. all of the above. none of the above. The point (0,4) is feasible. satisfies the first and second constraints but not the third. satisfies the first and third constraints but not the second. satisfies the second and third constraints but not the first. none of the above. The optimal solution of this linear programming model is (3,2) (4,0) (0,4) (8/5,21/5) (60/19,28/19) Assigning a value of 10 to the objective function, i.e., making 5x1+2x2=10, the line representing the objective function goes through the following two points (2,0) and (5,0) (0,2) and (5,0) (0,2) and (0,5) (2,0) and (0,5) none of the above The line representing the constraint 4x1+5x2=20 goes through the following two points (4,0) and (5,0) (5,0) and (4,0) (4,0) and (0,5) (0,4) and (0,5) none of the above The point (1,351) is feasible. satisfies the first constraint but not the second and third. satisfies the second constraint but not the first and third. satisfies the third constraint but not the first and second. none of the above