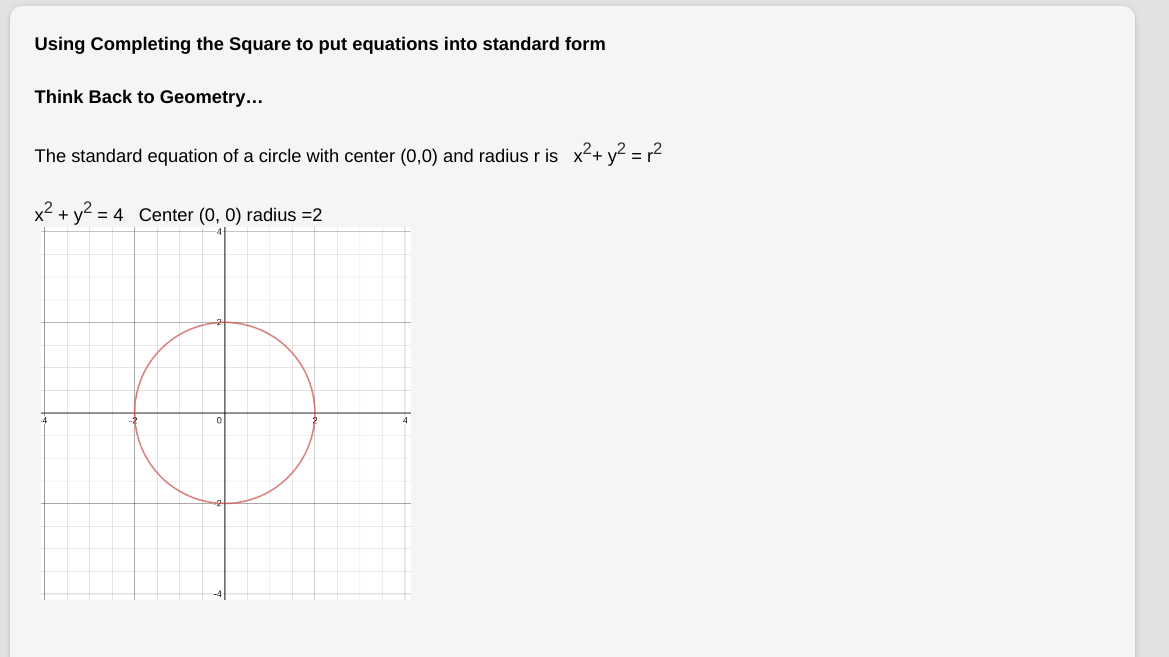
Question: Using Completing the Square to put equations into standard form Think Back to Geometry... 2 2_2 The standard equation of a circle with center (0,0)


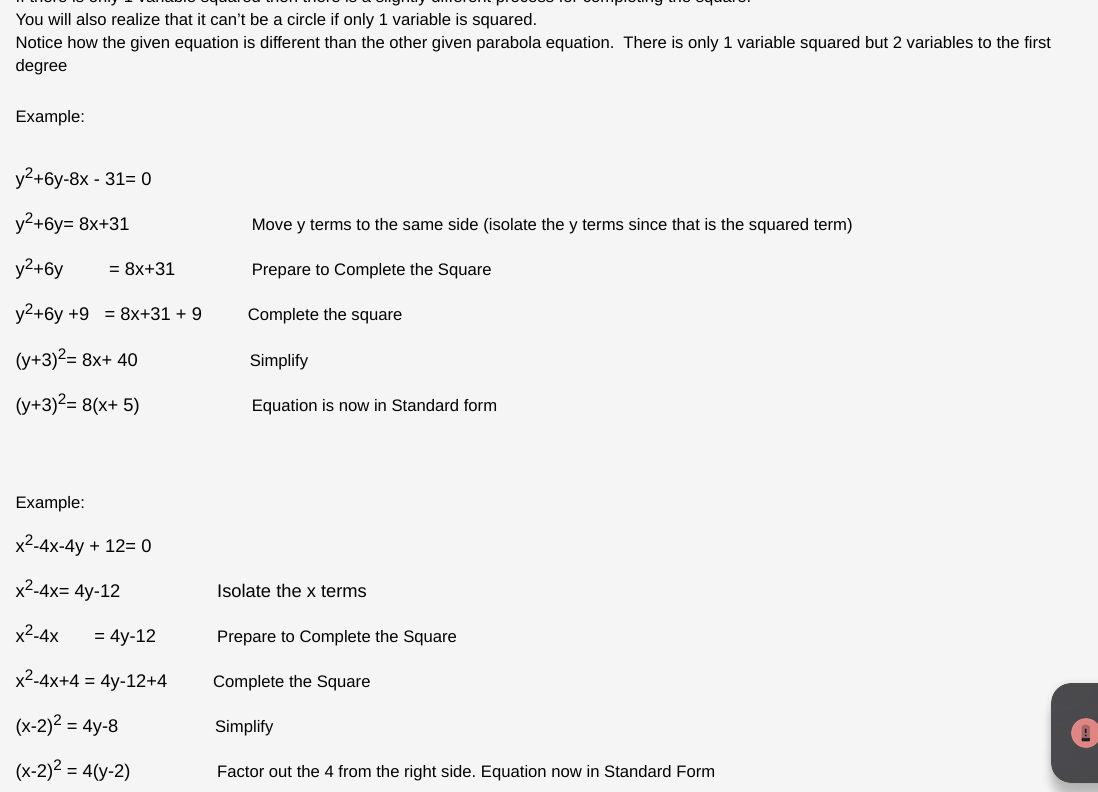
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


