Question: Using Fourier integral transforms solve the following. Let be the sine transform of where is the sine transform of and is the cosine transform of
Using Fourier integral transforms solve the following.
Let 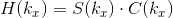 be the sine transform of
be the sine transform of 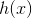 where
where 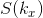 is the sine transform of
is the sine transform of 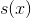 and
and ![Sky s(2 Cky / CCC h(x) = _[s(x)[(x+x")=c(x+x")]dx'=-=[c(*)[$(x+x")= s(x-x)]dx* Hk) = S(k).C(k)](https://s3.amazonaws.com/si.experts.images/answers/2024/08/66cceeec74684_54066cceeec27de6.jpg) is the cosine transform of
is the cosine transform of ![04 Sky s(2 Cky / CCC h(x) = _[s(x)[(x+x")=c(x+x")]dx'=-=[c(*)[$(x+x")= s(x-x)]dx*](https://s3.amazonaws.com/si.experts.images/answers/2024/08/66cceeed02483_54066cceeeca36b7.jpg) .
.
Suppose that 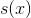 and
and 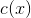 are odd and even functions respectively.
are odd and even functions respectively.
Show that
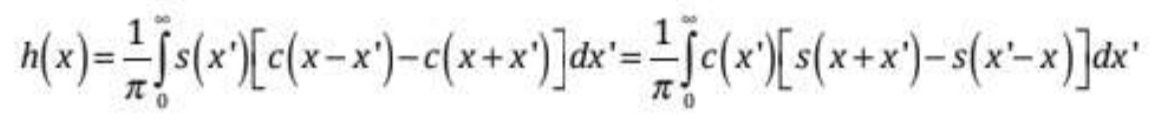
Where x' is the derivative of x.
Hk) = S(k).C(k) 04 Sky s(2 Cky / CCC h(x) = _[s(x)[(x+x")=c(x+x")]dx'=-=[c(*)[$(x+x")= s(x-x)]dx* Hk) = S(k).C(k) 04 Sky s(2 Cky / CCC h(x) = _[s(x)[(x+x")=c(x+x")]dx'=-=[c(*)[$(x+x")= s(x-x)]dx*
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


