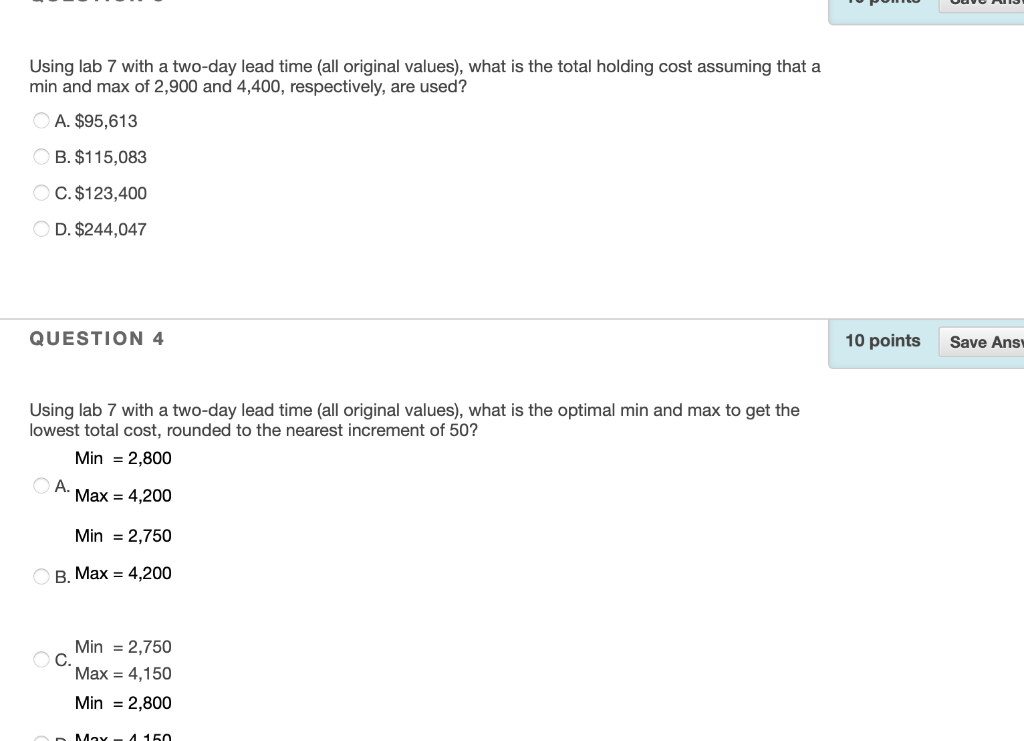
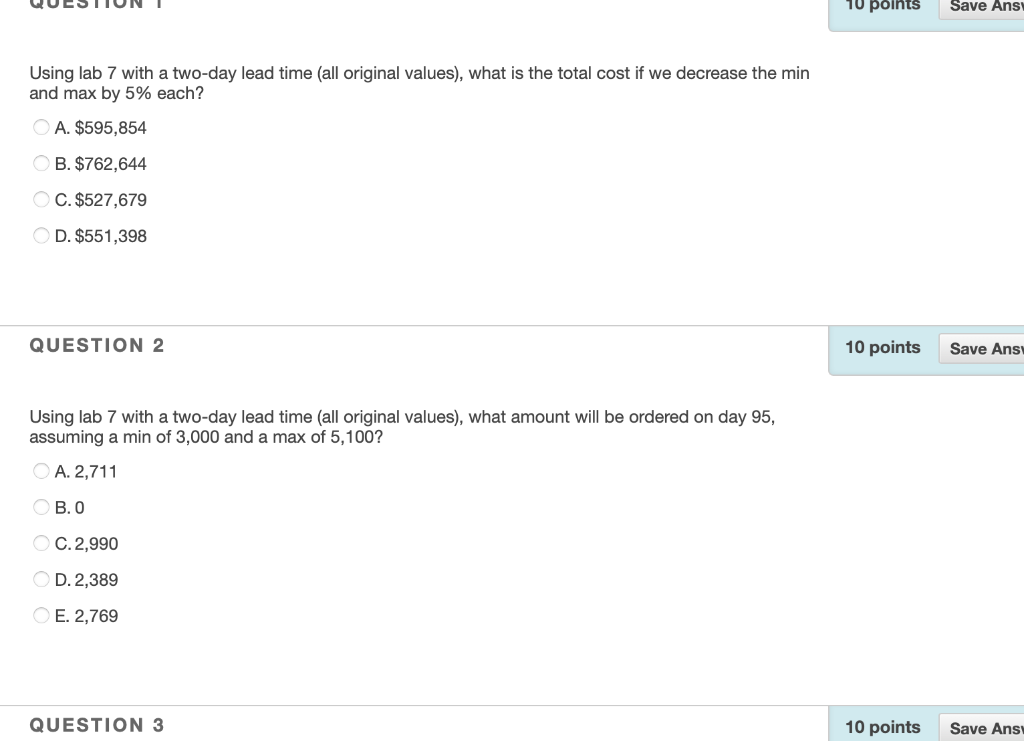
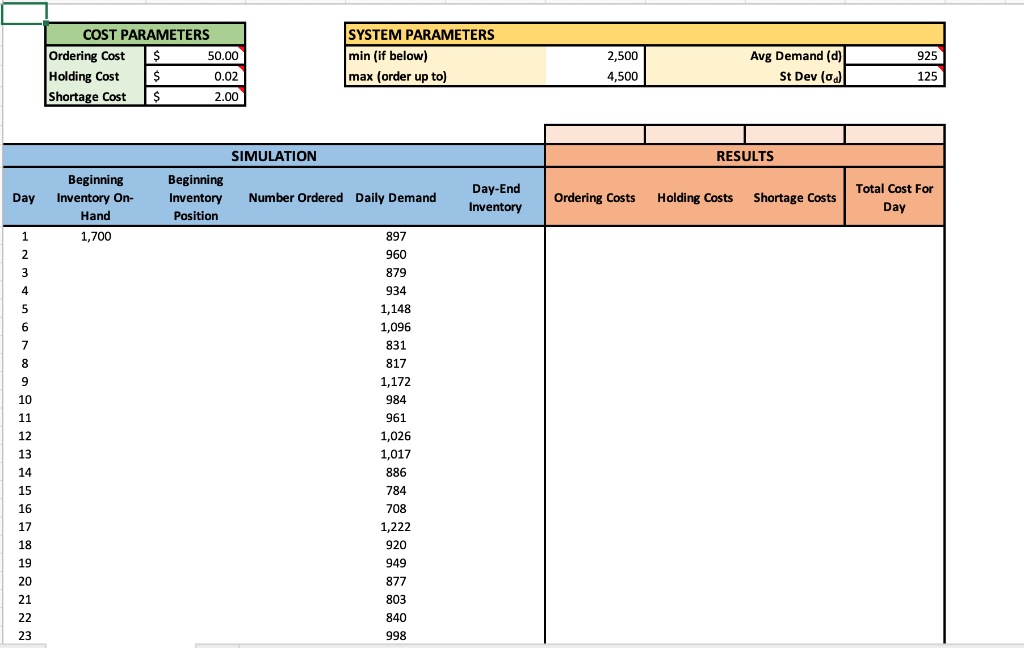
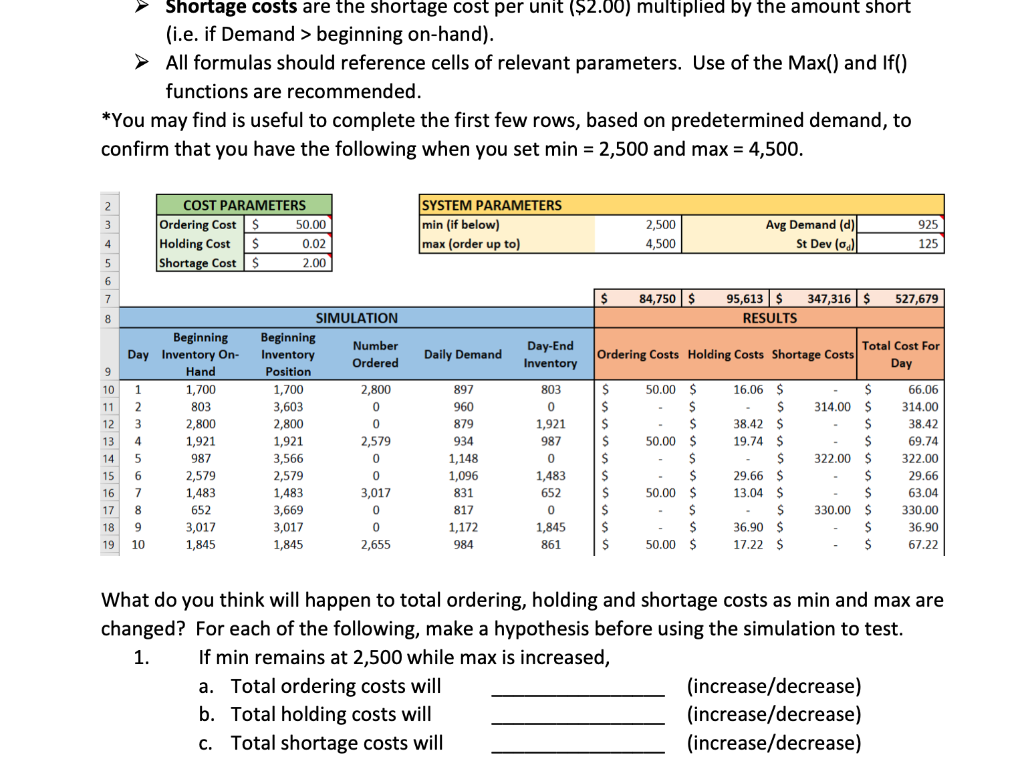
Using lab 7 with a two-day lead time (all original values), what is the total holding cost assuming that a min and max of 2,900 and 4,400, respectively, are used? A. $95,613 B. $115,083 C. $123,400 D. $244,047 QUESTION 4 10 points Save Ans Using lab 7 with a two-day lead time (all original values), what is the optimal min and max to get the lowest total cost, rounded to the nearest increment of 50? Min = 2,800 A. Max = 4,200 Min = 2,750 B. Max = 4,200 Min = 2,750 C. Max = 4,150 Min = 2,800 May150 10 points Save Ans Using lab 7 with a two-day lead time (all original values), what is the total cost if we decrease the min and max by 5% each? A. $595,854 B. $762,644 C. $527,679 D. $551,398 QUESTION 2 10 points Save Ans Using lab 7 with a two-day lead time (all original values), what amount will be ordered on day 95, assuming a min of 3,000 and a max of 5, 100? A. 2,711 B.O C. 2,990 D. 2,389 E. 2,769 QUESTION 3 10 points Save Ans COST PARAMETERS Ordering Cost $ 50.00 Holding Cost $ 0.02 Shortage Cost $ 2.00 SYSTEM PARAMETERS min (if below) max (order up to) Avg Demand (d) 2,500 4,500 925 125 ) St Dev SIMULATION RESULTS Day Beginning Inventory Position Number Ordered Daily Demand Day-End Inventory Ordering Costs Beginning Inventory On- Hand 1,700 Holding Costs Shortage Costs Total Cost For Day 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 897 960 879 934 1,148 1,096 831 817 1,172 984 961 1,026 1,017 886 784 708 1,222 920 949 877 803 840 998 21 22 23 QUESTION 5 10 points Save Ans Using lab 7 with a three-day lead time (all original values), what is the total cost with a min and max of 7,700 and 9,900, respectively? (Round your answer to the nearest whole number) Shortage costs are the shortage cost per unit ($2.00) multiplied by the amount short (i.e. if Demand > beginning on-hand). All formulas should reference cells of relevant parameters. Use of the Max() and if() functions are recommended. *You may find is useful to complete the first few rows, based on predetermined demand, to confirm that you have the following when you set min = 2,500 and max = 4,500. 2 3 COST PARAMETERS Ordering Costs 50.00 Holding Cost $ 0.02 Shortage Costs 2.00 SYSTEM PARAMETERS min (if below) max (order up to) 2,500 4,500 Avg Demand (d) St Dev (0) 925 125 4 5 5 6 7 $ 84,750 $ 95,613 S RESULTS 347,316 $ 527,679 8 Daily Demand Day-End Inventory Total Cost For Ordering Costs Holding Costs Shortage Costs Day 9 10 11 12 S $ $ SIMULATION Beginning Number Inventory Ordered Position 1,700 2,800 3,603 0 2,800 0 1,921 2,579 3,566 0 2,579 0 1,483 3,017 3,669 0 3,017 0 1,845 2,655 13 14 15 16 17 Beginning Day Inventory On- Hand 1 1,700 2 803 3 2,800 4 1,921 5 987 6 2,579 7 1,483 8 652 9 3,017 10 1,845 897 960 879 934 1,148 1,096 831 817 1,172 803 0 1,921 987 0 1,483 652 0 1,845 861 $ $ $ $ $ $ S 50.00 $ $ $ 50.00 $ $ $ 50.00 $ $ $ 50.00 $ $ 16.06 $ $ 38.42 $ 19.74 $ $ 29.66 S 13.04 $ $ 36.90 $ 17.22 $ $ 314.00 $ $ $ 322.00 $ $ $ 330.00 $ $ $ 66.06 314.00 38.42 69.74 322.00 29.66 63.04 330.00 36.90 67.22 18 19 984 What do you think will happen to total ordering, holding and shortage costs as min and max are changed? For each of the following, make a hypothesis before using the simulation to test. 1. If min remains at 2,500 while max is increased, a. Total ordering costs will (increase/decrease) b. Total holding costs will (increase/decrease) c. Total shortage costs will (increase/decrease)