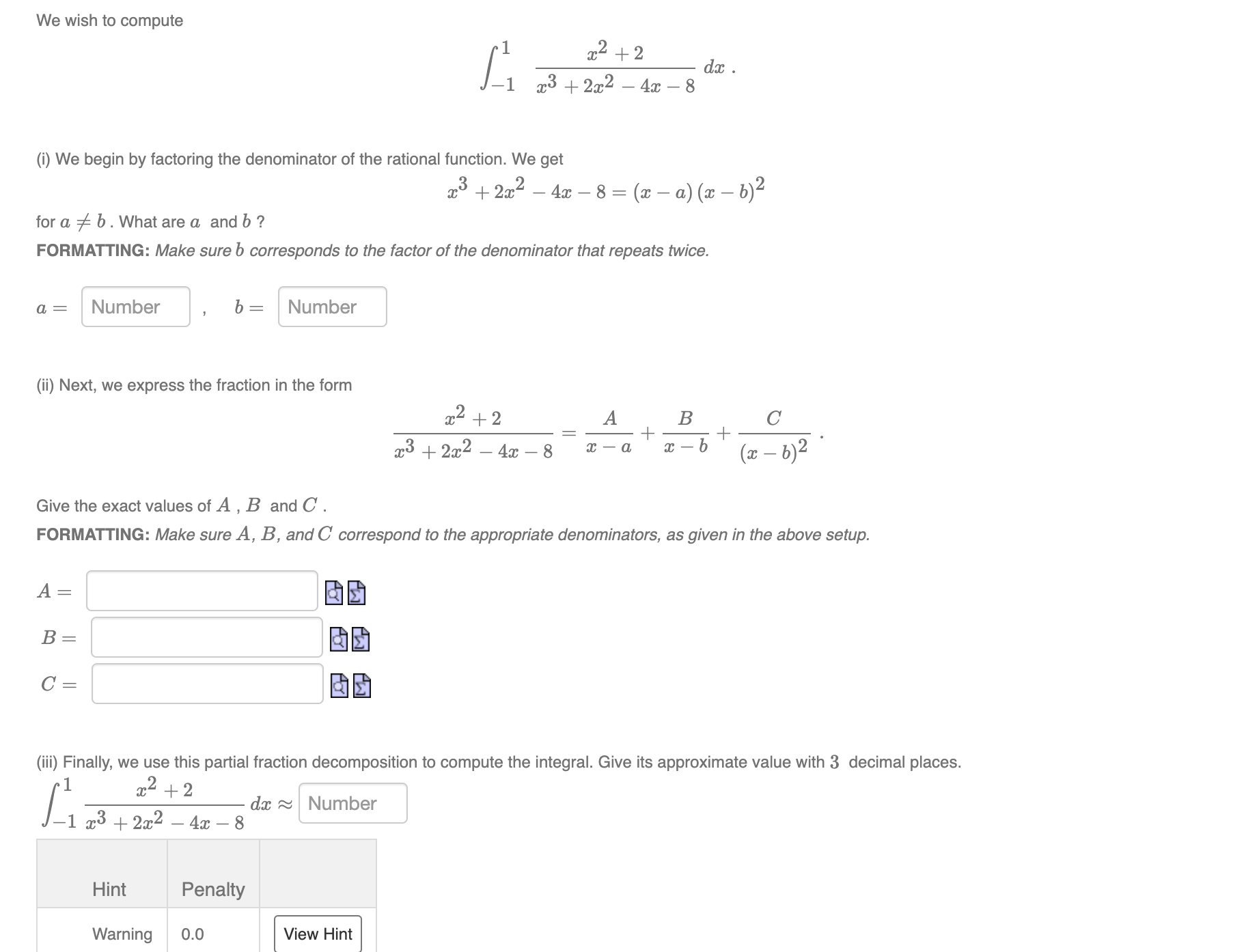
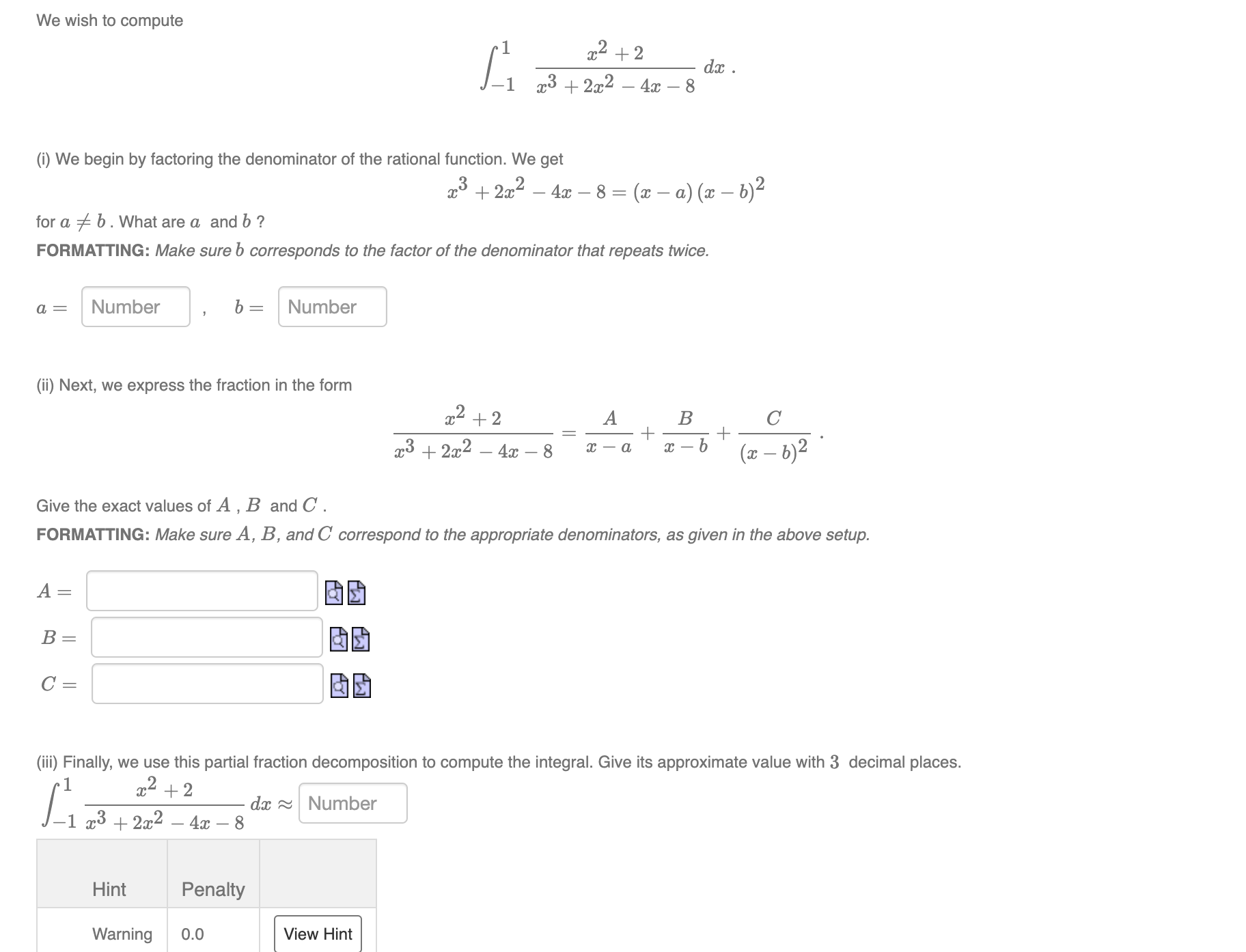
We wish to compute 202 + 2 dx . 23 + 2x2 - 4x - 8 (i) We begin by factoring the denominator of the rational function. We get 23 + 2x - 4x - 8 = (2 - a) (2-6)2 for a # b . What are a and b ? FORMATTING: Make sure b corresponds to the factor of the denominator that repeats twice. a = Number b = Number (ii) Next, we express the fraction in the form 2 2 + 2 A B C + 23 + 2x2 - 4x -8 x - a x - (a - 6)2 Give the exact values of A , B and C . FORMATTING: Make sure A, B, and C correspond to the appropriate denominators, as given in the above setup. A = B = C = (iii) Finally, we use this partial fraction decomposition to compute the integral. Give its approximate value with 3 decimal places. 202 + 2 da ~ Number 1 23 + 2x2 - 4x - 8 Hint Penalty Warning 0.0 View Hint