What would be the step by step solutions be for these?

What is rewritten is the correction. The second picture is the chart we were given. Im not quite sure what all it is asking is to answer as well.

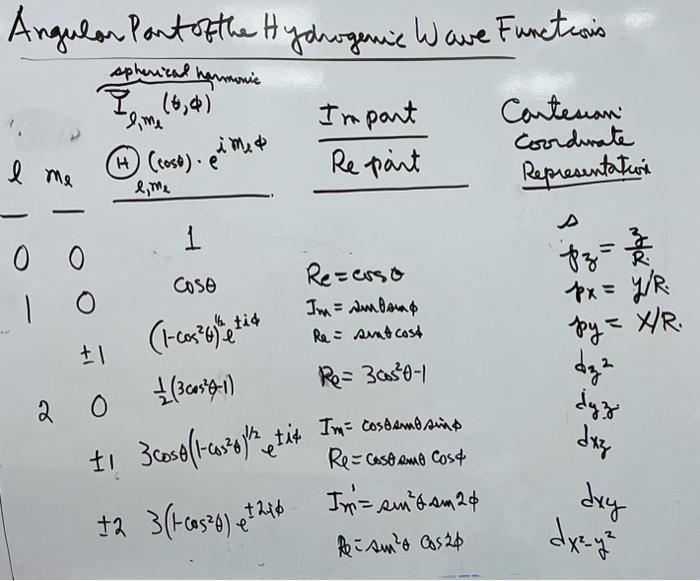
2. Below is a list of spherical harmonics, Y(,) which are used to represent the angular dependence of the electron wave function in a hydrogen atom, as well as the electron wave functions in atoms of higher atomic number. The angle arguments, and , in Ylm(,), are the spherical polar angles. Consider a sphere of unit radius, so that the corresponding Cartesian coordinates are z=cos , x=sincos and y=sinsin. For each of the Ylm(,) listed below, separate the real and imaginary parts, where they occur, and identify the corresponding Cartesian electron orbital that is generated. As a guide, cases (a) and (b) list the Cartesian orbitals corresponding to the p-states. (a) =1,m=0,Y10(,)=cos. Because =1, this is a p-orbital. Because z=cos, it corresponds to a pz - orbital in Cartesian form. (b) =1,m=1,Y11(,)=3cossine. Because =1, and m=1, this Y11(,) generates two p-orbitals. Re[Y11(,)]=3sincos, corresponds to a px - orbital Im[Y11(,)]=3sinsin, corresponds to a py - orbital (c) The following Ym(,) generate the d-orbitals, dz2,dxzdxy,dyz, and dx2y2. Below in Eqs.(1) - (3) are the spherical harmonics corresponding to =2 Y20(,)=21(3cos21)Y21(,)=cossineiY22(,)=sin2e2i Identify which of the Y22(,) in Eqs.(1) - (3) is the parent for each Cartesian dorbitals listed above. 2. Below is a list of spherical harmonics, Ym(,) which are used to represent the angular dependence of the electron wave function in a hydrogen atom, as well as the electron wave functions in atoms of higher atomic number. The angle arguments, and , in Yfm(,), are the spherical polar angles. Consider a sphere of unit radius, so that the corresponding Cartesian coordinates are z=cos x=sincos and y=sinsin. For each of the Ymm(,) listed below, separate the real and imaginary parts, where they occur, and identify the corresponding Cartesian electron orbital that is generated. As a guide, cases (a) and (b) list the Cartesian orbitals corresponding to the p-states. (a) =1,m=0,Y10(,)=cos. Because =1, this is a p-orbital. Because z=cos, it corresponds to a pz - orbital in Cartesian form. (b) =1,m=1,Y11(,) sososinge ei. Because =1, and m=1, this Y11(,) generates two p-orbitals. Re[Y11(,)]=3sincos, corresponds to a px - orbital Im[Y11(,)]=3sinsin, corresponds to a py - orbital (c) The following Ym(,) generate the d-orbitals, dy2,dxzdxy,dyz, and dx2y2. Below in Eqs.(1) - (3) are the spherical harmonics corresponding to =2 Y20(,)=21(3cos21)Y21(,)=cossine1Y22(,)=sin2e2i Identify which of the Y22(,) in Eqs.(1) - (3) is the parent for each Cartesian dorbitals listed above. Angulon Pant of the Hydrogenic Wave Functesis