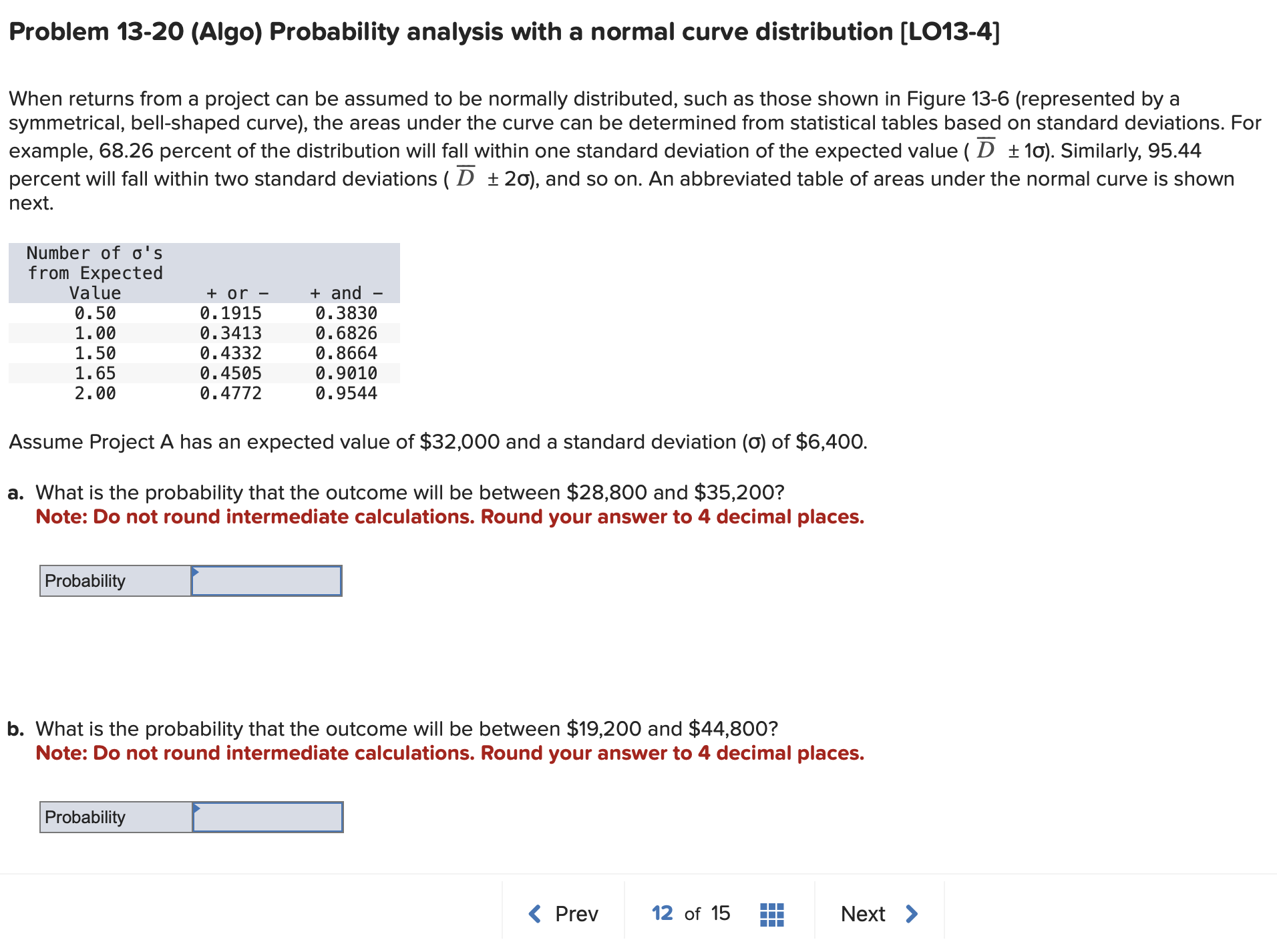
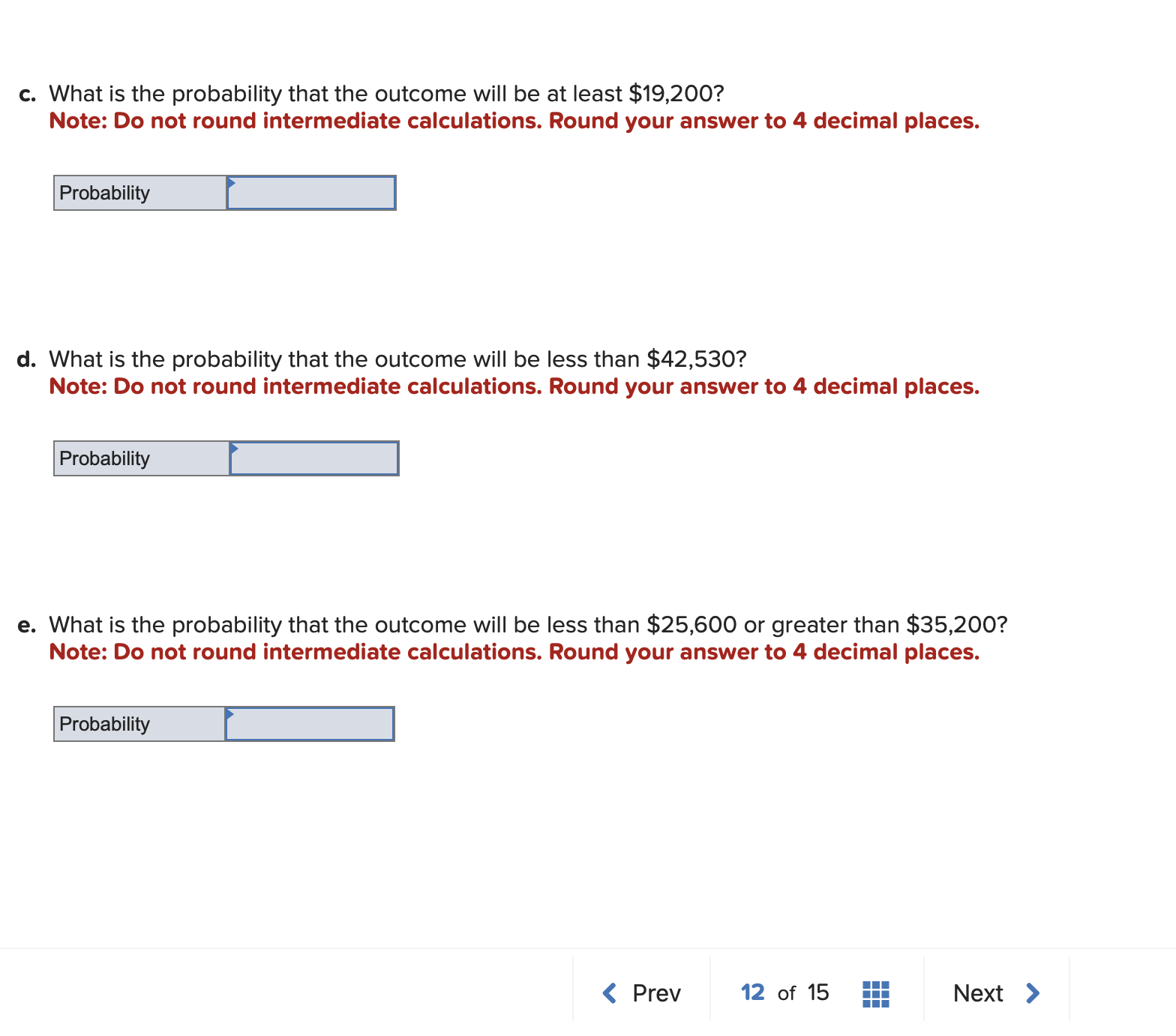
When returns from a project can be assumed to be normally distributed, such as those shown in Figure 13-6 (represented by a symmetrical, bell-shaped curve), the areas under the curve can be determined from statistical tables based on standard deviations. For example, 68.26 percent of the distribution will fall within one standard deviation of the expected value ( D1). Similarly, 95.44 percent will fall within two standard deviations ( D2), and so on. An abbreviated table of areas under the normal curve is shown next. a. What is the probability that the outcome will be between $28,800 and $35,200 ? Note: Do not round intermediate calculations. Round your answer to 4 decimal places. b. What is the probability that the outcome will be between $19,200 and $44,800 ? Note: Do not round intermediate calculations. Round your answer to 4 decimal places. c. What is the probability that the outcome will be at least $19,200 ? Note: Do not round intermediate calculations. Round your answer to 4 decimal places. d. What is the probability that the outcome will be less than $42,530 ? Note: Do not round intermediate calculations. Round your answer to 4 decimal places. e. What is the probability that the outcome will be less than $25,600 or greater than $35,200 ? Note: Do not round intermediate calculations. Round your answer to 4 decimal places. When returns from a project can be assumed to be normally distributed, such as those shown in Figure 13-6 (represented by a symmetrical, bell-shaped curve), the areas under the curve can be determined from statistical tables based on standard deviations. For example, 68.26 percent of the distribution will fall within one standard deviation of the expected value ( D1). Similarly, 95.44 percent will fall within two standard deviations ( D2), and so on. An abbreviated table of areas under the normal curve is shown next. a. What is the probability that the outcome will be between $28,800 and $35,200 ? Note: Do not round intermediate calculations. Round your answer to 4 decimal places. b. What is the probability that the outcome will be between $19,200 and $44,800 ? Note: Do not round intermediate calculations. Round your answer to 4 decimal places. c. What is the probability that the outcome will be at least $19,200 ? Note: Do not round intermediate calculations. Round your answer to 4 decimal places. d. What is the probability that the outcome will be less than $42,530 ? Note: Do not round intermediate calculations. Round your answer to 4 decimal places. e. What is the probability that the outcome will be less than $25,600 or greater than $35,200 ? Note: Do not round intermediate calculations. Round your answer to 4 decimal places