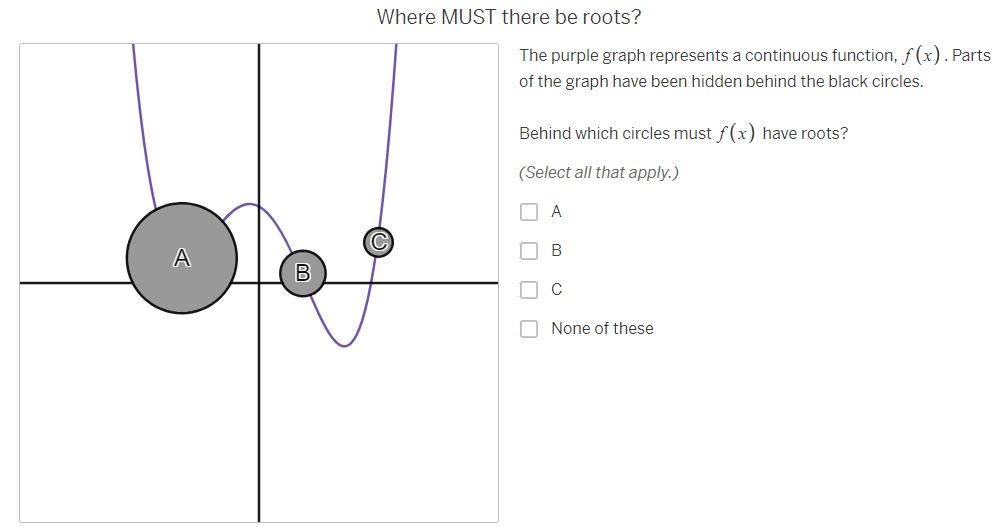
Question: Where MUST there be roots? The purple graph represents a continuous function, f (x) . Parts of the graph have been hidden behind the black
![[J]c [ ] None of thase Where MUST there be roots? The](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/670a3b3260a0c_762670a3b32431e2.jpg)
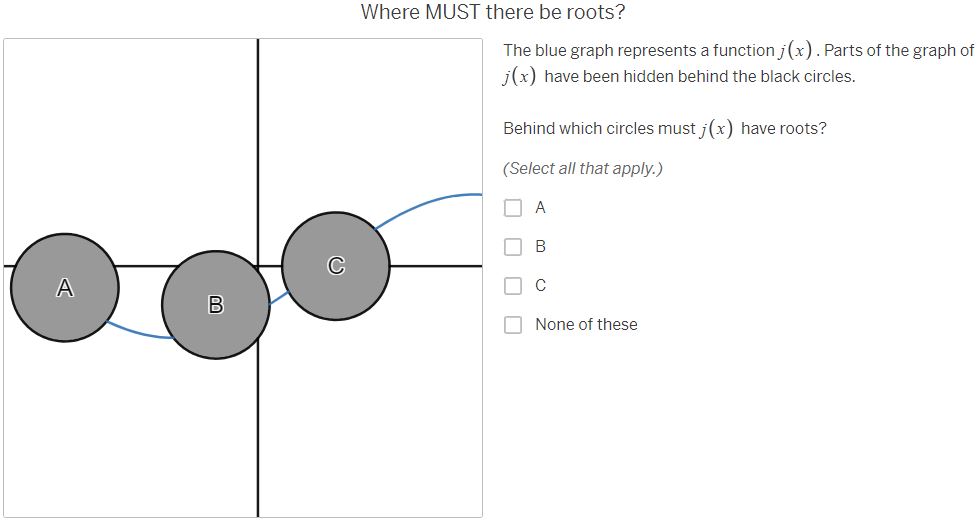
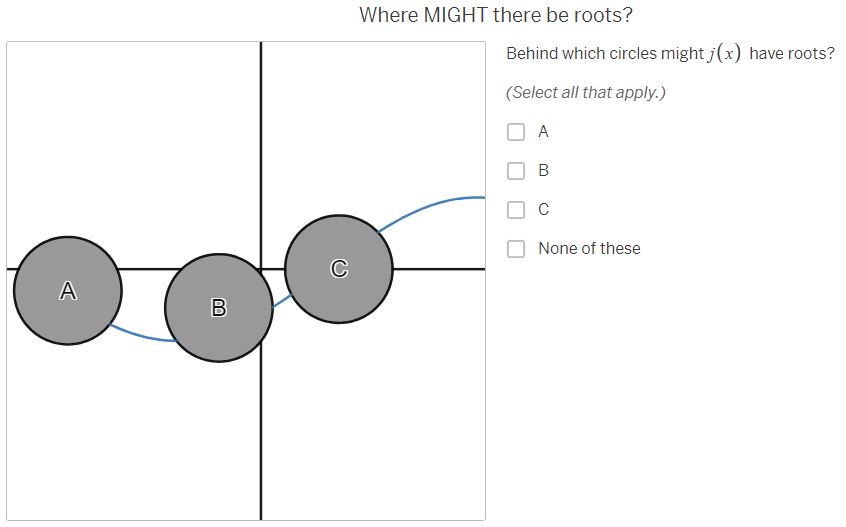
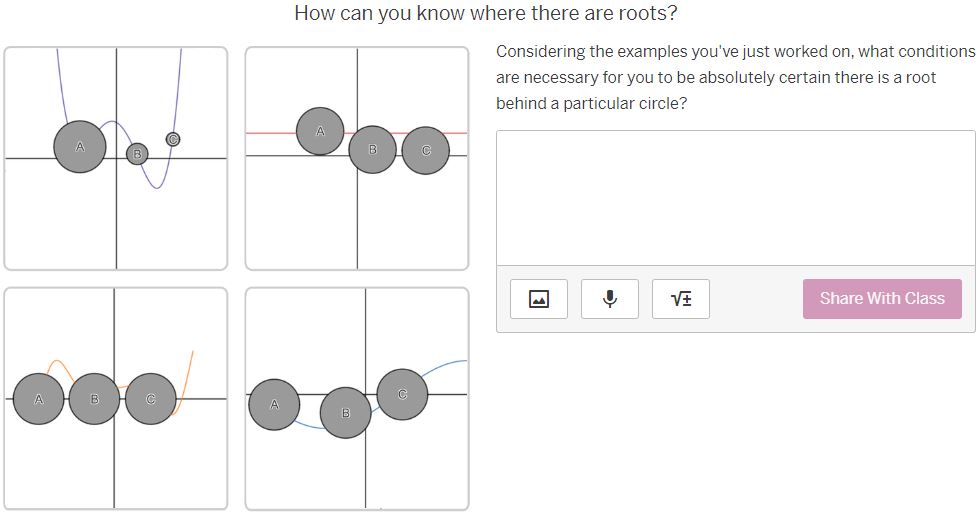
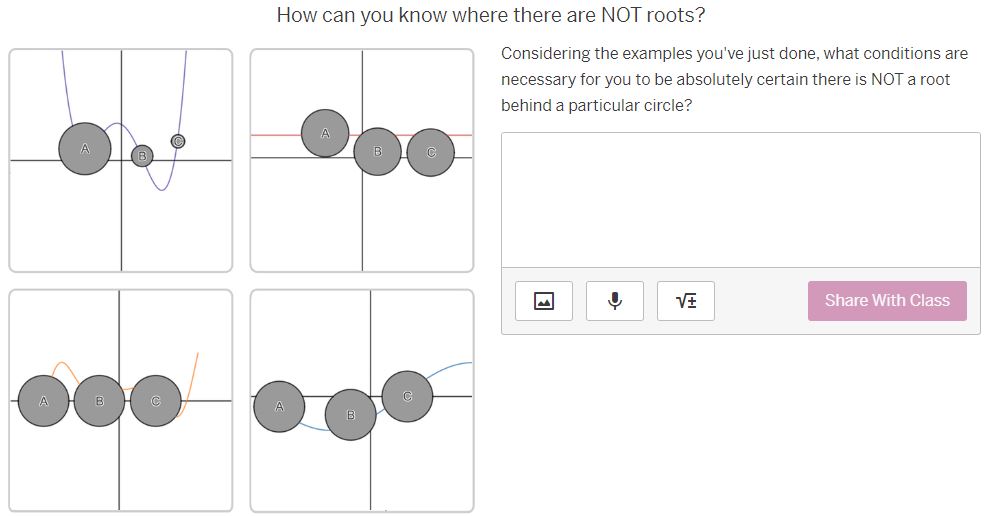
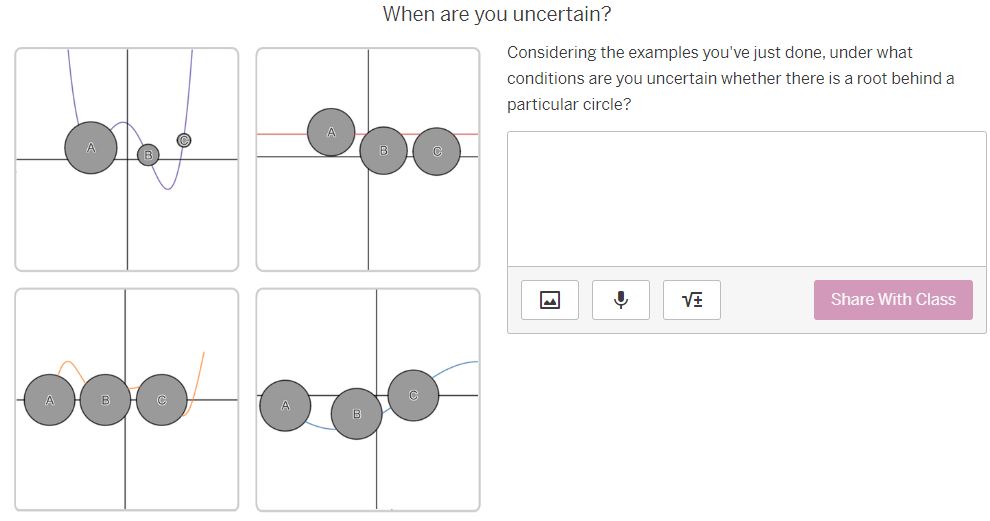
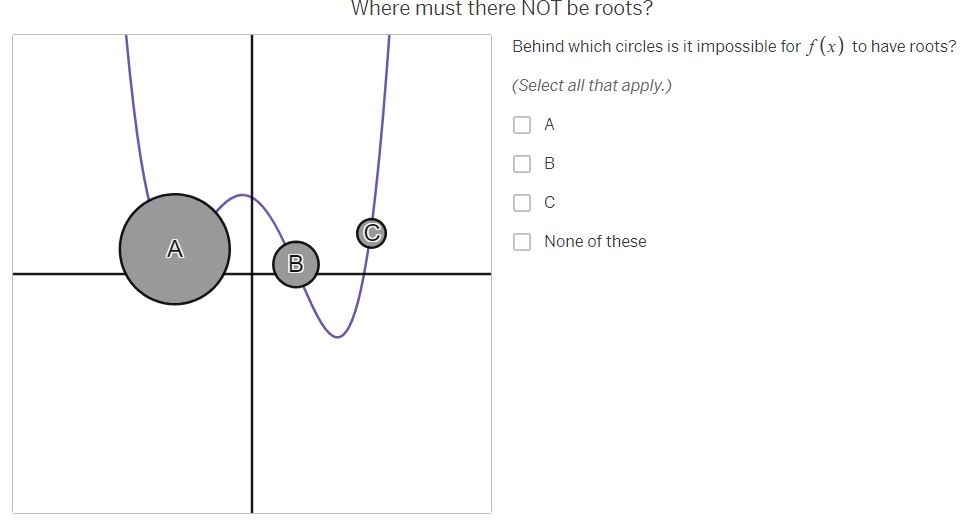
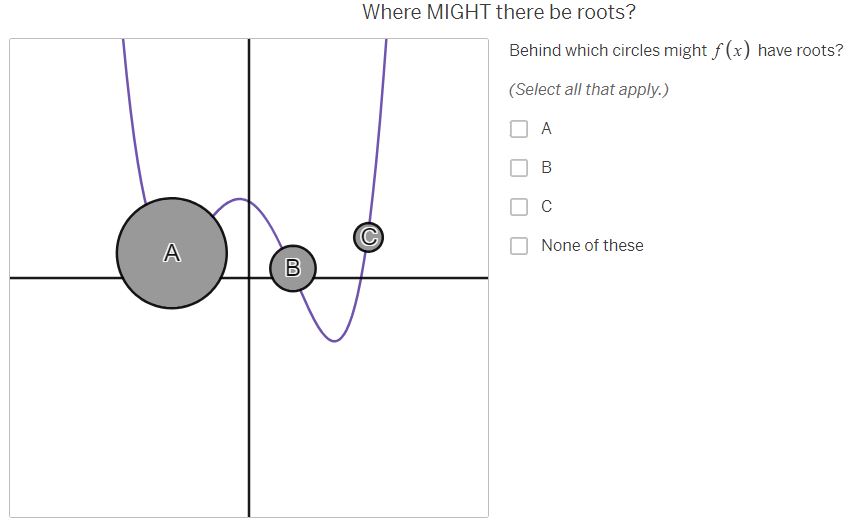
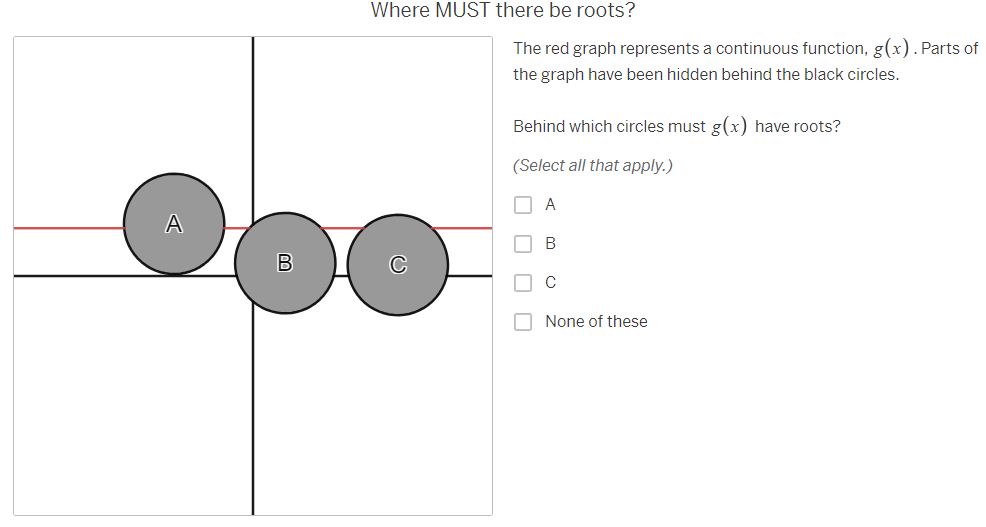
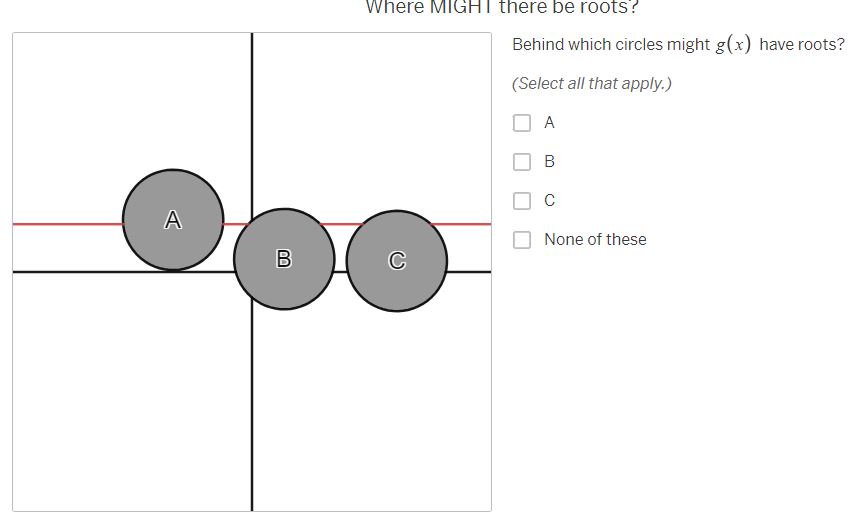
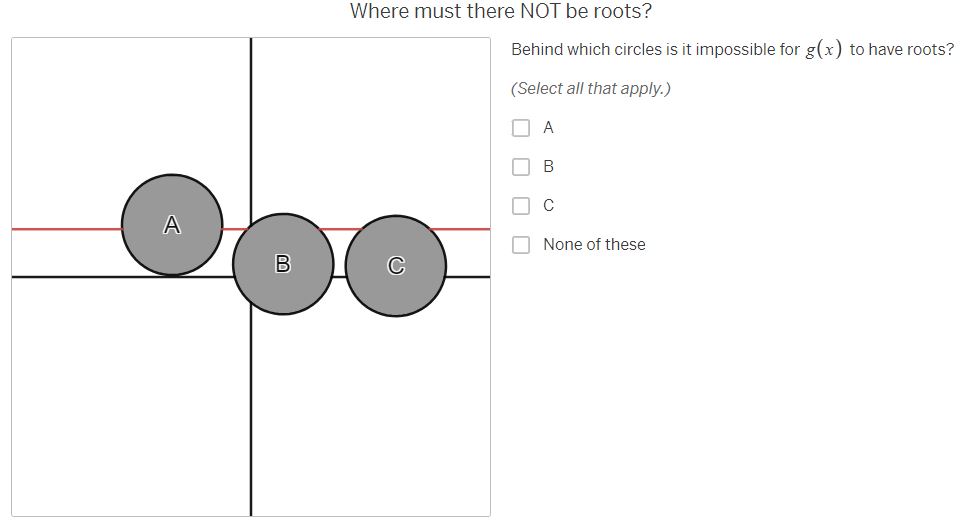
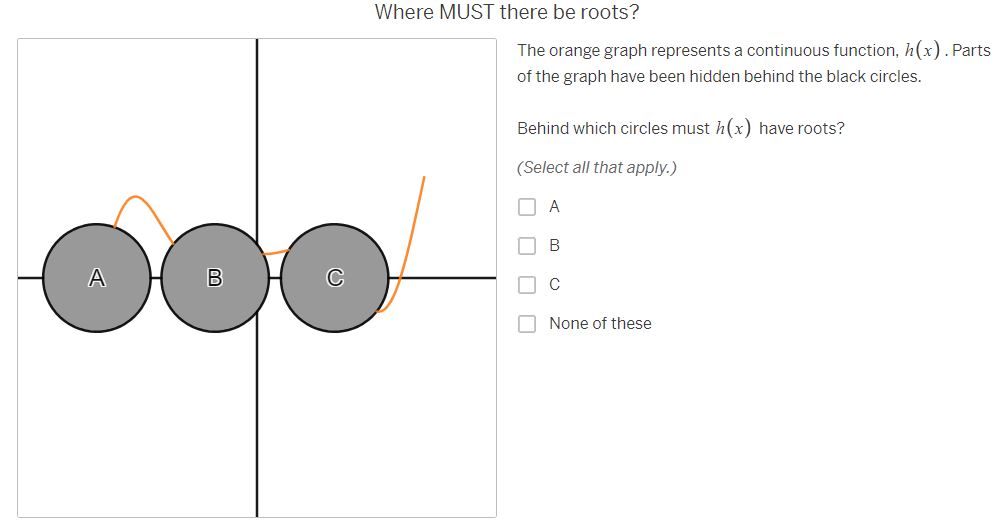
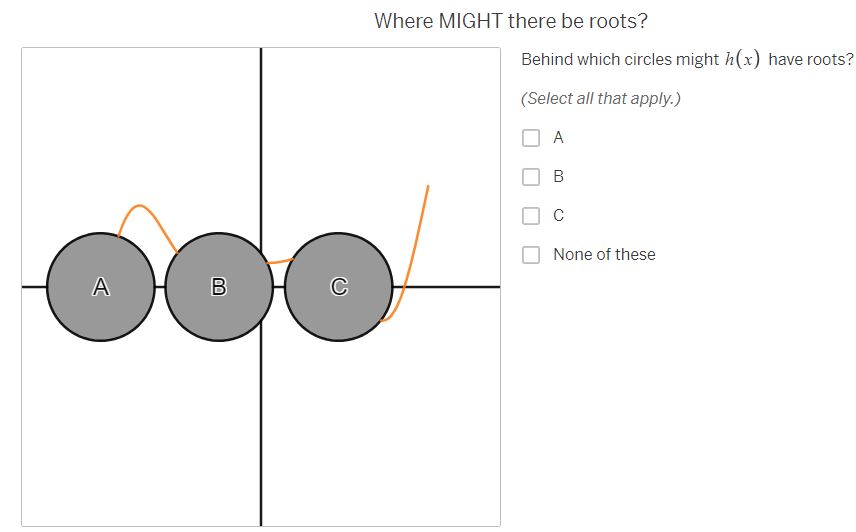
Where MUST there be roots? The purple graph represents a continuous function, f (x) . Parts of the graph have been hidden behind the black circles. Behind which circles must f (x ) have roots? (Select all that apply.) A A B B C None of theseWhere must there NOT be roots? Behind which circles is it impossible for f (x ) to have roots? (Select all that apply.) A B C A None of these BWhere MIGHT there be roots? Behind which circles might f(x) have roots? (Select all that apply.) O A B [J]c [ ] None of thase Where MUST there be roots? The red graph represents a continuous function, g(x) . Parts of the graph have been hidden behind the black circles. Behind which circles must g(x) have roots? (Select all that apply.) O e None of these Where MIGH | there be roots? Behind which circles might g(x) have roots? (Select all that apply.) A O B C C | MNone of these Where must there NOT be roots? Behind which circles is it impossible for g(x ) to have roots? (Select all that apply.) A B C A None of these B CWhere MUST there be roots? The orange graph represents a continuous function, h(x] .Parts of the graph have been hidden behind the black circles. Behind which circles must i(x) have roots? (Select all that apply.) 0 A R Jc [} None of these Where MIGHT there be roots? Behind which circles might h (x ) have roots? (Select all that apply.) A B C None of these B CWhere must there NOT be roots? Behind which circles is it impossible for h(x) to have roots? (Select all that apply.) O A [0 B O & MNone of these Where MUST there be roots? The blue graph represents a function j{x] . Parts of the graph of 7(x) have been hidden behind the black circles. Behind which circles must j(x) have roots? (Select all that apply.) O A [ B O c None of these Where MIGHT there be roots? Behind which circles might j(x) have roots? (Select all that apply.) A dc None of these How can you know where there are roots? Considering the examples you've just worked on, what conditions are necessary for you to be absolutely certain there is a root behind a particular circle? ' [l H & H Vi ' Share With Class How can you know where there are NOT roots? Considering the examples you've just done, what conditions are necessary for you to be absolutely certain there is NOT a root behind a particular circle? | = H & H Vi | Share With Class When are you uncertain? Considering the examples you've just done, under what conditions are you uncertain whether there is a root behind a particular circle? A A B C V+ Share With Class A B
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


