Question: Which graph is the slope field for dy/dx = sin x , cos x What is the antiderivative of g(x) = 3* that contains the
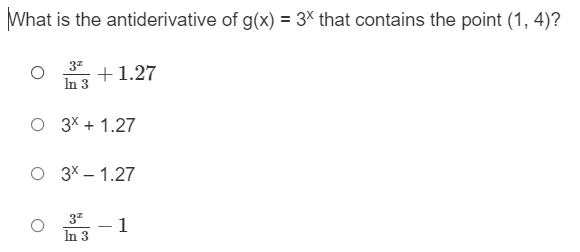


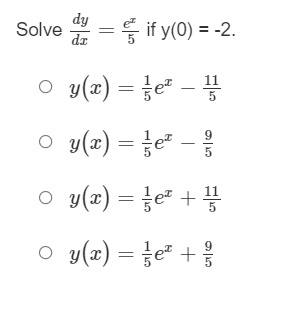

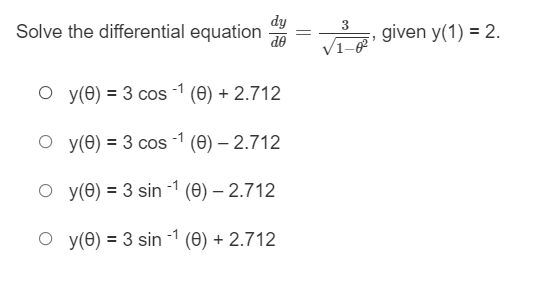

![3tan' (t) +3 - 5 O y(t) = 2tan] (t) +3 -](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6667f99682e75_1346667f9965b507.jpg)
![O y (t) = tan] (t) +3 - 5\fIf f (0) =](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6667f996f3e43_1346667f996d2748.jpg)
Which graph is the slope field for dy/dx = sin x , cos x
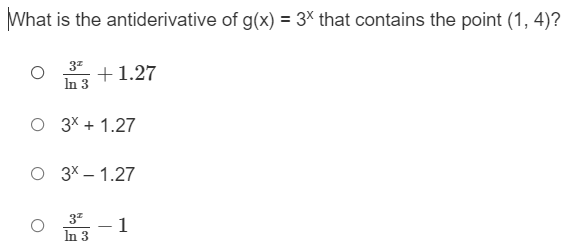


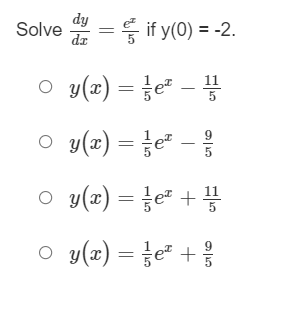

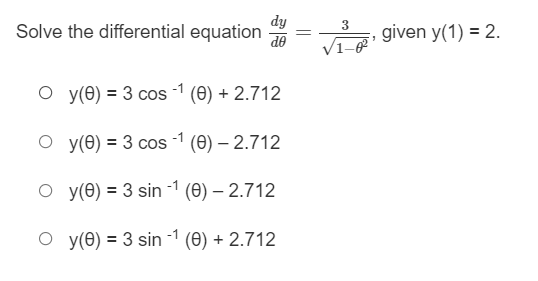

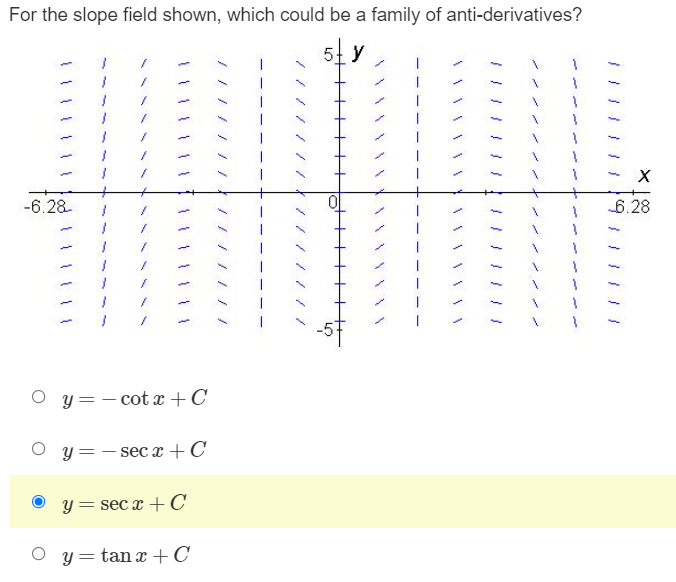
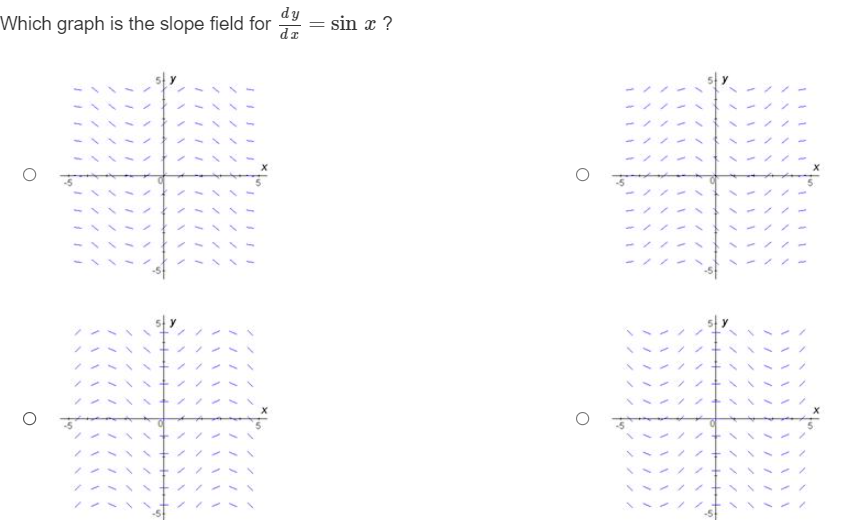
What is the antiderivative of g(x) = 3* that contains the point (1, 4)? O In 3 + 1.27 O 3* + 1.27 O 3% - 1.27 O In 3\fWhat is the equation of the curve that passes through the point (1, 3) and has a slope at any point defined by y ' = -2 1+ +2 ? O y(t) = 2tan' (t) +3 + O y(t) = 3tan' (t) +3 - 5 O y(t) = 2tan] (t) +3 - O y (t) = tan] (t) +3 - 5\fIf f (0) = 2, what is the particular antiderivative of f'(x) = 4 sec2x? O f (x) = -4 cot x + 2 Of (x) = -4 tan x + 2. Of (x) = -4 tan x Of (x) = 4 tan x + 2.\fFor the slope field given, which equation could be a family of anti-derivatives? X -6.28 6.28 O y = cosx + C O y = sinx + C O y = tana + C O y= -tana + CFor the slope field shown, which could be a family of anti-derivatives? 5 1 1 1 1 1 1 1 1 X -6.28 6.28 1711711 114171 1 161 1 1 1 -5 O y= - cota +C O y= -seca + C O y = secx + C O y = tanx + C
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


