Write a python program that will calculate the function e^x . Make sure your program meets the following requirements:

1. The value of x can be specified and changed in the code (or as user input).

2. The value of x0 can be specified and changed in the code (or as user input).

3. Your program should continue to calculate the Talyor series until 1010 .

4. Demonstrate your program works correctly by running it for the following case: x0 = 0.0, x = 4.0.

5. Use program to use base points, x0 = 0.0, 0.5, 1.5, 2.0, 2.5, 3.0, 3.5 and x = 4.0 to determine the number of terms, N required to get an answer that has 1010 1.

6.Make a graph of N versus h (Note h = x-x0).

I have already done #1-4 with the following code:

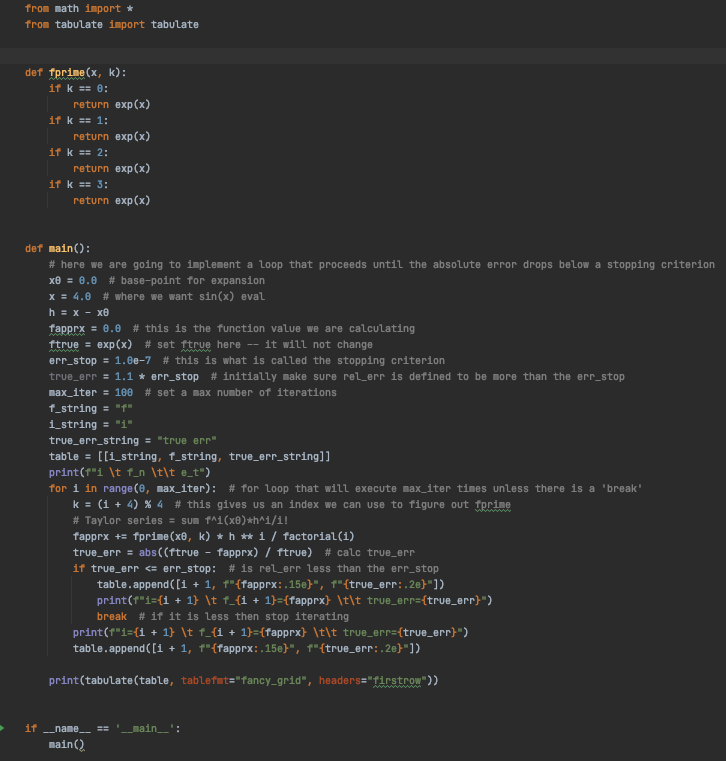However, I am not sure how to do #5. This is where. I need help -- thank you very much

edit: nevermind, I think I have figured out the problem:

I just need to run the program for all those Xo values to see how many terms they produce until getting to a precision of 10^-10, and then for each h (4.0 - 0.0, 4.0 - 3.5, 4.0 - 3.0, etc.) will be a different value for the graph along with its N number of terms?

from math import * from tabulate import tabulate def fprine(x, k): if k == 0: return exp(x) if kas 1: return exp(x) if k == 2: return exp(x) if k == 3: return exp(x) def main(); # here we are going to implement a loop that proceeds until the absolute error drops below a stopping criterion x = 8.6 # base-point for expansion x= 4.0 # where we want sin(x) eval h = x - x0 fapprx = 0.0 # this is the function value we are calculating ftrue = exp(x) # set ftrue here -- it will not change err_stop = 1.6e-7 # this is what is called the stopping criterion true_err = 1,1 * err_stop # initially make sure rel_err is defined to be more than the err_stop max_iter = 180 # set a max number of iterations f_string = "1" 1_string = "1" true_err_string = "true err" table = [[i_string, f_string, true_err_string]] print("1 \t fun \t\t e_t") for i in range(e, max_iter): # for loop that will execute max_iter times unless there is a 'break' k = (i + 4) % 4 # this gives us an index we can use to figure out fprime # Taylor series = sum f^i(x0) h^i/i! fapprx += Tprime(xe, k) * h ** i/ factorial(1) true_err = abs((ftrue fapprx) / ftrue) # calc true_err if true_err