1. Write the governing ordinary differential equation for the steady, one dimensional (x direction) convection and diffusion of , in a given one dimensional uniform flow field u. The fluid density is and diffusion coefficient is . Then, write the continuity equation in terms of and u.

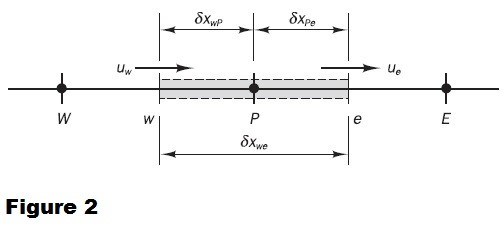
1. Integrate the transport and the continuity equations over the one-dimensional control volume shown in Figure 2. Using central differencing for the diffusive terms obtained by integration, and linear interpolation to compute the cell face values for the convective terms, assuming a uniform grid spacing, obtain the discretized steady convection-diffusion equation in one space dimension (x) by the finite volumes approach.

2. Integrate the transport and the continuity equations over the one-dimensional control volume shown in Figure 2. Using central differencing for the diffusive terms obtained by integration, and linear upwind interpolation (upwind differencing scheme, UDS) for the convective terms, assuming a uniform grid spacing, obtain the discretized steady convection-diffusion equation in one space dimension (x) by the finite volumes approach.

3. Integrate the transport and the continuity equations over the one-dimensional control volume shown in Figure 2. Using central differencing for the diffusive terms obtained by integration, and quadratic upwind interpolation for the convective kinematics (QUICK), assuming a uniform grid spacing, obtain the discretized steady convection-diffusion equation in one space dimension (x) by the finite volumes approach.

8xpe ue w W e E Figure 2 8xpe ue w W e E Figure 2