Write the python code : I was able to do 1 and 2 but i dont know about the rest.

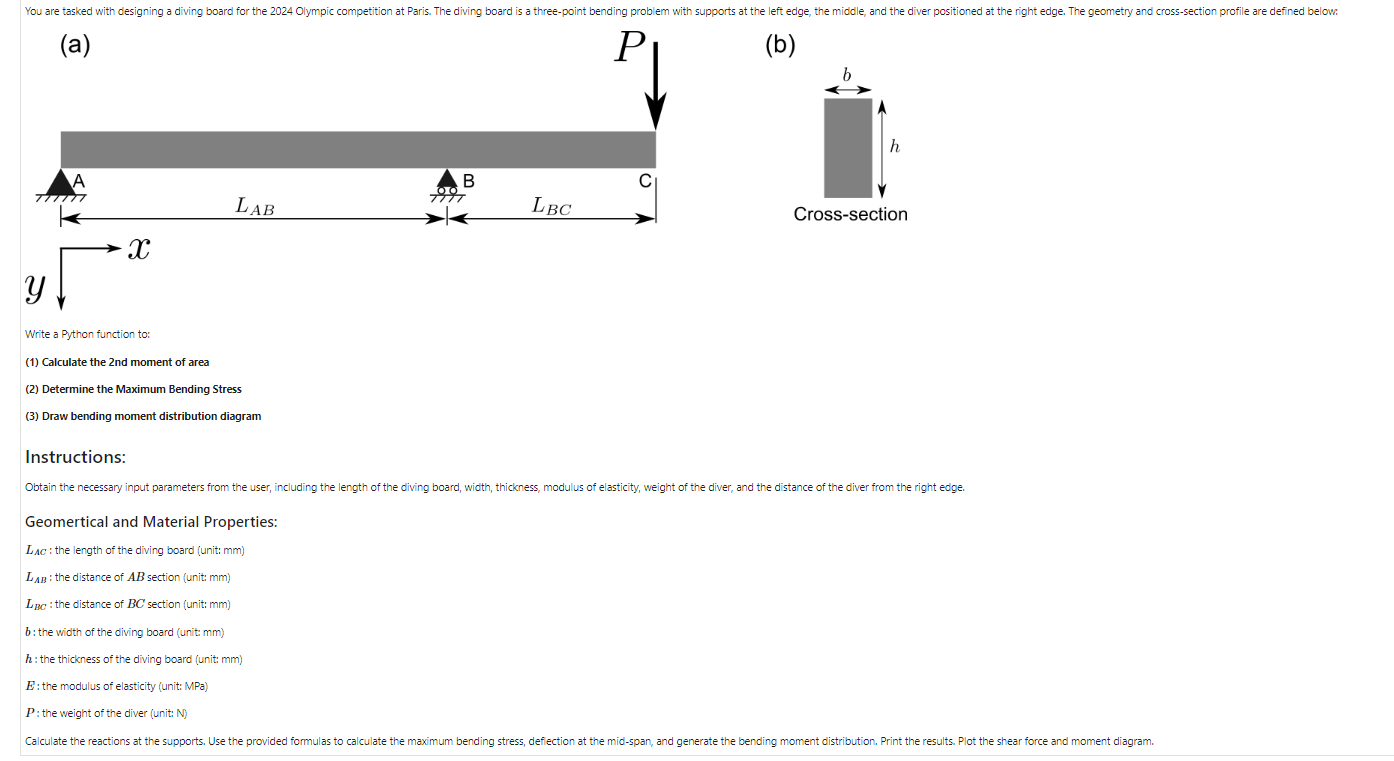
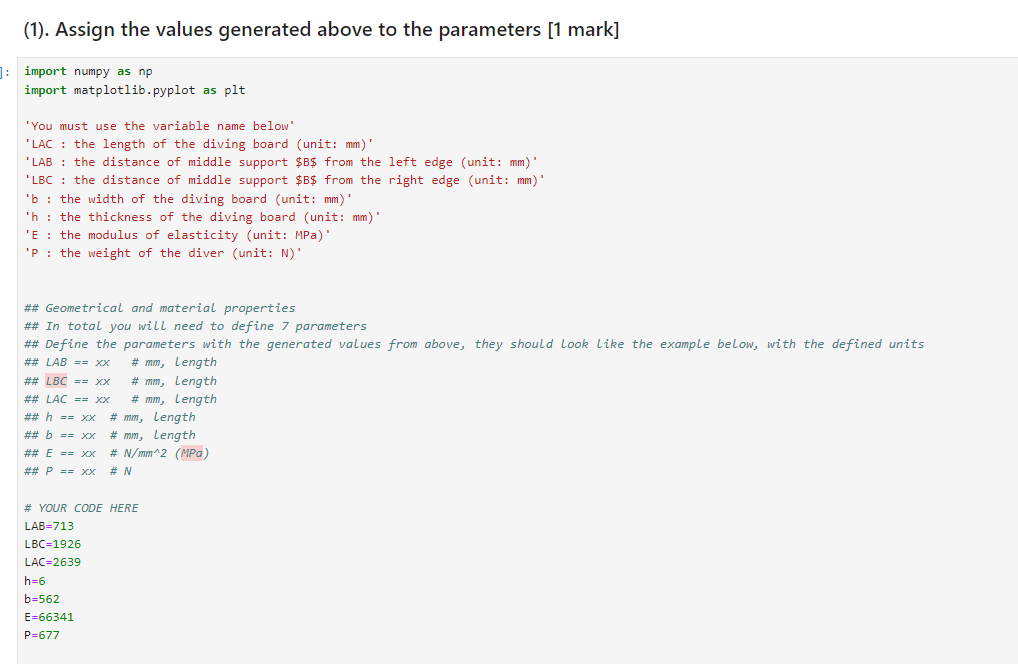
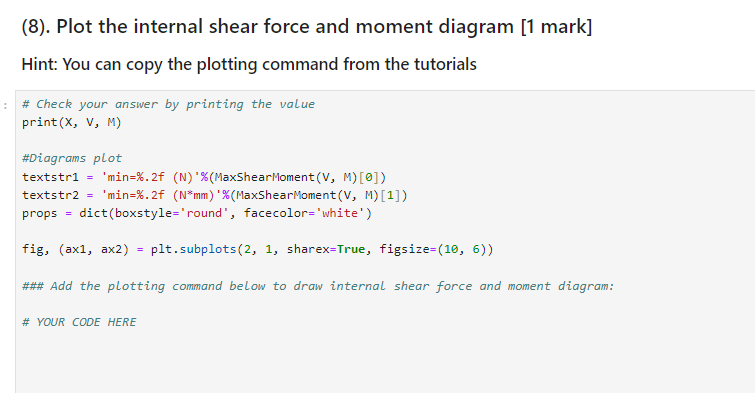
Write a Python function to: (1) Calculate the 2nd moment of area (2) Determine the Maximum Bending Stress (3) Draw bending moment distribution diagram Instructions: Geomertical and Material Properties: LAC : the length of the diving board (unit: mm ) LAB : the distance of AB section (unit: mm ) LBC : the distance of BC section (unit: mm ) b : the width of the diving board (unit: mm) h : the thickness of the diving board (unit: mm) E : the modulus of elasticity (unit: MPa) P : the weight of the diver (unit: N ) (1). Assign the values generated above to the parameters [1 mark] import numpy as np import matplotlib.pyplot as plt 'You must use the variable name below' 'LAC : the length of the diving board (unit: mm)' 'LAB : the distance of middle support $B$ from the left edge (unit: mm)' 'LBC : the distance of middle support $B$ from the right edge (unit: mm )' ' b : the width of the diving board (unit: mm)' 'h : the thickness of the diving board (unit: mm)' 'E : the modulus of elasticity (unit: MPa)' 'P : the weight of the diver (unit: N )' \#\# Geometrical and material properties \#\# In total you will need to define 7 parameters \#\# Define the parameters with the generated values from above, they should look like the example below, with the defined units #AB==xx#mm, length ##BC==xx#mm, length #AC=xx# mm, length ##==xx#mm, length ##b=xx#mm, length #E=x#N/mm2 (MPa) ##=xx#N \# YOUR CODE HERE LAB=713 LBC=1926 LAC=2639 h=6 b=562 E=66341 P=677 (2). Define a function to calculate the 2nd moment of area [1 mark] \#\# Define a function to calculate the 2nd moment of area def SecondMomentArea (b,h) : \# YOUR CODE HERE I=((b)(h3))/12 | #print(fI={I0},I1={I1},I={I}) return I \# Check your answer by printing the value print("The 2nd moment of area=", SecondMomentArea(b,h)) The 2 nd moment of area =10116.0 (3). Find the support reaction forces at x=0 [1 marks] \#Reaction force or moment 'You must use the variable names YAadYB ' ' Y A ' Y B : Reaction force at the support point B' def ReactionForce(LAC, LAB, P): \# YOUR CODE HERE YA=0 YB=0 YA=P(LACP)/LAB YB=(LACP)/LAB return YA, YB \# Check your answer by printing the value print ("Y_A=", ReactionForce(LAC, LAB, P) [0], "Y_ B= ", Reactionforce(LAC, LAB, P) [1] ) YA=1828.7545582047687YB=2505.7545582047687 (4). Find the expression for internal force V and moments M at AB. [3 marks] 'You must use the variable names P, LAC, LAB, x,V and M' - LAC: The total beam length AC (mm) ' ' LAB: The beam length AB (mm) ' P: Load (N)' ' x : arbitrary poistion along the beam ( mm )" ' V: Array of Shear force (N)' - M: Array of Internal moment (N*mm)' \# Define the shear force and bending moment arrays X=np. linspace (,LAC, num=LAC, endpoint=True) V=npzeros(LAC) M=npzeros(LAC) def ABDiagram(LAC, LAB, P): for x in range ( , LAB ) : \# YOUR CODE HERE return V,M \# Check your answer by printing the value print("V=", ABDiagram(LAC, LAB, P) [ 0], "M=", ABDiagram(LAC, LAB, P) [1]) (5). Find the expression for internal force V and moments M at BC. [3 marks] 'You must use the variable names P,LAC,LAB,x,V and M ' ' LAC: The total beam length AC (mm) ' - LAB: The beam length AB (mm) - LBC : The beam length BC (mm) ' P: Load (N)' ' x : arbitrary poistion along the beam ( mm )" - V: Array of Shear force (N) ' - M: Array of Internal moment ( Nmm) " def BCDiagram(LAC, LAB, P): for x in range (LAB, LAC): \# YOUR CODE HERE return V,M \# Check your answer by printing the value print("V=", BCDiagram(LAC, LAB, P) [0], "M=", BCDiagram(LAC, LAB, P) [1]) 'Use the variable names maxV and maxM below:' ' maxV: Maximum shear force (N)' ' maxM: Maximum internal moment ( N mm) " def MaxShearMoment (V,M) : \# YOUR CODE HERE return maxV,maxM \# Check your answer by printing the values print ('max shear force=', MaxShearMoment (V,M)[0] ) print ('max moment=', MaxShearMoment (V, M) [1]) (7). Find the maximum bending stress [1 mark] - You must use the variable names maxM, yc and I' ' maxM: Maximum internal moment ( Nmm) ' 'yc: the distance between the maximum stress point and the neutual plane (mm)" ' I: the 2nd moment of area' I=SecondMomentArea(b,h)maxMM=MaxShearMoment(V,M)[1]yc=h/2 def MaxBendingStress(maxM, yc, I): \# YOUR CODE HERE return SigmaB \# Check your answer by printing the value print('Maxium Bending stress=', MaxBendingstress(maxM, yc, I), 'MPa') (8). Plot the internal shear force and moment diagram [1 mark] Hint: You can copy the plotting command from the tutorials \# Check your answer by printing the value print(X,V,M) \#Diagrams plot textstr1 =min=%.2f(N)%( MaxShearMoment (V,M)[0]) textstr2 = 'min=\%.2f ( N mm )%( MaxShearMoment (V,M)[1]) props = dict (boxstyle=' round ', facecolor='white') fig, (ax1, ax2) = plt.subplots (2,1, sharex=True, figsize=(10, 6)) \#\# Add the plotting command below to draw internal shear force and moment diagram: \# YOUR CODE HERE