(x a) = x-a when x is greater then or equal to a

(x-a) = 0 when x is less than a

Here is the complete code:

clc;

clear;

i = 1;

for x = 0:0.5:360

if x less than or equal to 120

d(i) = 800*x^3-13.68*10^6*x-2.5*x^4;

i = i+1;

else

if x less than or equal to 240

d(i) = 800*x^3-13.68*10^6*x-2.5*x^4+2.5*(x-120)^4;

i = i+1;

else

d(i) = 800*x^3-13.68*10^6*x-2.5*x^4+2.5*(x-120)^4+600*(x-240)^3;

i = i+1;

end

end

end

x = 0:0.5:360;

deflection = (1/(3.190*10^9))*d;

% Calculating Max Absolute value and Position x(index)

[max_diflection,index] = max(abs(deflection));

fprintf("Max absolute Diflection is %d at x = %d",max_diflection,x(index));

plot(x,deflection);

title('Deflection of beam under load'); xlabel('Position on beam [in.]'); ylabel('Deflection of beam [in.]');

% converting into tabular form

x = x';

deflection = deflection';

T = table(x,deflection)

I need the part of the problem that says

The program should also print the distances and deflections to an external txt file as a neat table. If someone could edit the same code and do this it will be of great help

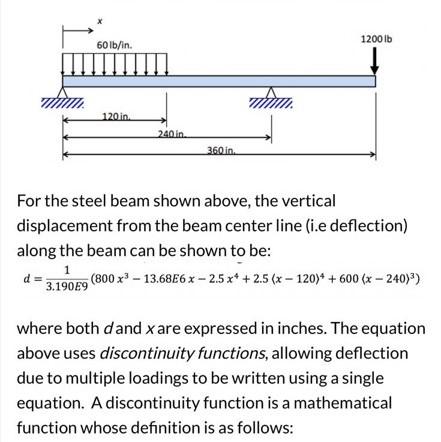
For the steel beam shown above, the vertical displacement from the beam center line (i.e deflection) along the beam can be shown to be: d=3.190E91(800x313.68E6x2.5x4+2.5x1204+600x2403) where both d and x are expressed in inches. The equation above uses discontinuity functions, allowing deflection due to multiple loadings to be written using a single equation. A discontinuity function is a mathematical function whose definition is as follows: where a is any real number. For example, in the equation for displacement above, there are two discontinuity functions used, one with a equal to 120 and the other with a equal to 240 . Design and write a Matlab program that calculates the deflected shape of the above beam and finds the maximum deflection (as an absolute value) and its location ( x value). To do this, calculate the deflections for a vector of discrete points along the beam, with 1/2-inch increments. The program should also print the distances and deflections to an external text file as a neat table with distances in one column and deflections in a 2nd column, and should graph the deflection versus distance along the beam. You are required to use loop(s) to achieve both the discontinuity calculations and file output printing. For file output printing, you must use lower-level matlab functions (fopen, fprintf, fclose). To plot a graph of d versus x, you can use the command plot (x,d), where x and d are both vectors of the same length