You are given the expected return, volatility and correlation matrix assumptions for seven asset classes. Your first task is to plot the minimum variance frontier -- that is the locus of portfolio combinations that have the minimum risk for a given level of expected return. Assume there is no short-selling; in other words, your portfolio weights cannot be negative. (Hint: You can choose the option in Excel solver to make non-constrained variables non-negative.)

1. To construct the minimum variance frontier, first solve for the portfolio weights for the global minimum variance (GMV) portfolio. Compute the expected return, volatility and the Sharpe ratio of this portfolio.
2. Next, solve for the portfolio weights for the mean variance efficient (MVE) portfolio. Compute the expected return, volatility and the Sharpe ratio of this portfolio.

Given the two GMV and the MVE portfolios you have identified, now construct the minimum variance frontier by computing the expected return and volatility for various combinations of these two portfolios. Note that you will also need to compute the variance/covariance matrix and the correlation between these two portfolios.

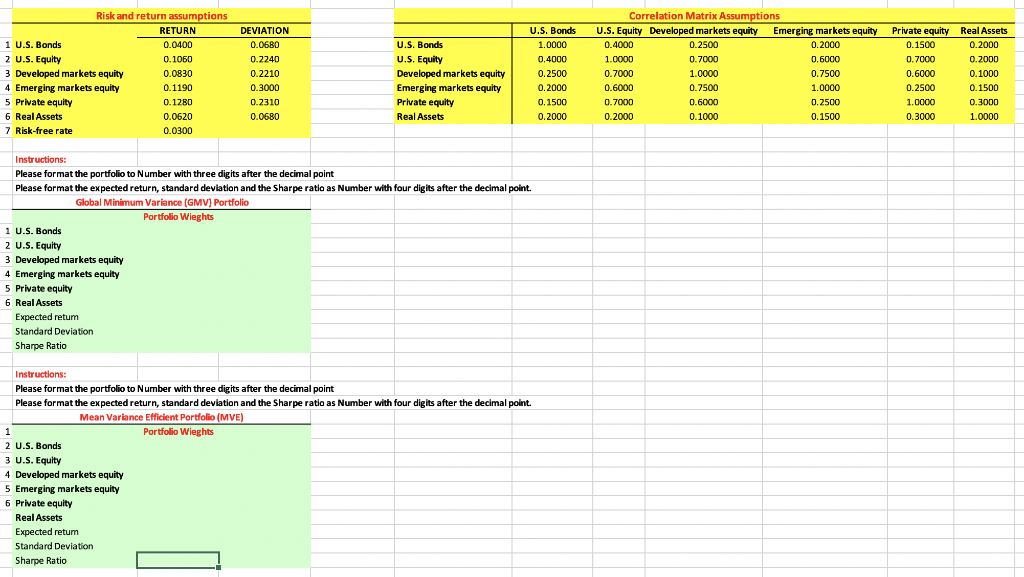
Risk and return assumptions RETURN 1 U.S. Bonds 0.0400 2 U.S. Equity 0.1060 3 Developed markets equity 0.0830 4 Emerging markets equity 0.1190 5 Private equity 0.1280 6 Real Assets 0.0620 7 Risk-free rate 0.0300 DEVIATION 0.0680 0.2240 0.2210 0.3000 0.2310 0.0680 U.S. Bonds U.S. Equity Developed markets equity Emerging markets equity Private equity Real Assets U.S. Bonds 1.0000 0.4000 0.2500 0.2000 0.1500 0.2000 Correlation Matrix Assumptions U.S. Equity Developed markets equity Emerging markets equity 0.4000 0.2500 0.2000 1.0000 0.7000 0.6000 0.7000 1.0000 0.7500 0.6000 0.7500 1.0000 0.7000 0.6000 0.2500 0.2000 0.1000 0.1500 Private equity 0.1500 0.7000 0.6000 0.2500 1.0000 0.3000 Real Assets 0.2000 0.2000 0.1000 0.1500 0.3000 1.0000 Instructions: Please format the portfolio to Number with three digits after the decimal point Please format the expected return, standard deviation and the Sharpe ratio as Number with four digits after the decimal point. Global Minimum Variance (GMV) Portfolio Portfolio Wieghts 1 U.S. Bonds 2 U.S. Equity 3 Developed markets equity 4 Emerging markets equity 5 Private equity 6 Real Assets Expected retum Standard Deviation Sharpe Ratio Instructions: Please format the portfolio to Number with three digits after the decimal point Please format the expected return, standard deviation and the Sharpe ratio as Number with four digits after the decimal point. Mean Variance Efficient Portfolio (MVE) Portfolio Wieghts 2 U.S. Bonds 3 U.S. Equity 4 Developed markets equity 5 Emerging markets equity 6 Private equity Real Assets Expected retum Standard Deviation Sharpe Ratio Risk and return assumptions RETURN 1 U.S. Bonds 0.0400 2 U.S. Equity 0.1060 3 Developed markets equity 0.0830 4 Emerging markets equity 0.1190 5 Private equity 0.1280 6 Real Assets 0.0620 7 Risk-free rate 0.0300 DEVIATION 0.0680 0.2240 0.2210 0.3000 0.2310 0.0680 U.S. Bonds U.S. Equity Developed markets equity Emerging markets equity Private equity Real Assets U.S. Bonds 1.0000 0.4000 0.2500 0.2000 0.1500 0.2000 Correlation Matrix Assumptions U.S. Equity Developed markets equity Emerging markets equity 0.4000 0.2500 0.2000 1.0000 0.7000 0.6000 0.7000 1.0000 0.7500 0.6000 0.7500 1.0000 0.7000 0.6000 0.2500 0.2000 0.1000 0.1500 Private equity 0.1500 0.7000 0.6000 0.2500 1.0000 0.3000 Real Assets 0.2000 0.2000 0.1000 0.1500 0.3000 1.0000 Instructions: Please format the portfolio to Number with three digits after the decimal point Please format the expected return, standard deviation and the Sharpe ratio as Number with four digits after the decimal point. Global Minimum Variance (GMV) Portfolio Portfolio Wieghts 1 U.S. Bonds 2 U.S. Equity 3 Developed markets equity 4 Emerging markets equity 5 Private equity 6 Real Assets Expected retum Standard Deviation Sharpe Ratio Instructions: Please format the portfolio to Number with three digits after the decimal point Please format the expected return, standard deviation and the Sharpe ratio as Number with four digits after the decimal point. Mean Variance Efficient Portfolio (MVE) Portfolio Wieghts 2 U.S. Bonds 3 U.S. Equity 4 Developed markets equity 5 Emerging markets equity 6 Private equity Real Assets Expected retum Standard Deviation Sharpe Ratio