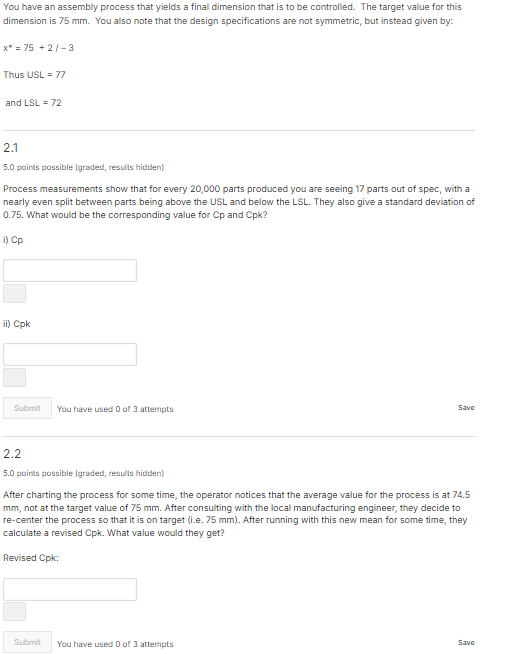
You have an assembly process that yields a final dimension that is to be controlled. The target value for this dimension is $75$ mm $.$ You also note that the design specifications are not symmetric, but instead given by:

$\backslash [$

$\backslash$mathrm$\{$x$\}^\{*\}=75+2/-3$

$\backslash ]$

Thus USL $\backslash (=77\backslash )$

and $\backslash (\backslash$mathrm$\{$LSL$\}=72\backslash )$

$2\mathrm{.}1$

$5\mathrm{.}0$ points possible $[$graded$,$ results hidden$)$

Process measurements show that for every $20,000$ parts produced you are seeing $17$ parts out of spec, with a nearly even split between parts being above the USL and below the LSL$.$ They also give a standard deviation of $0\mathrm{.}75.$ What would be the corresponding value for Cp and Cpk $?$

i$)$ Cp

ii$)$ Cpk

$2\mathrm{.}2$

$5\mathrm{.}0$ points possible $[$graded$,$ results hidden$)$

After charting the process for some time, the operator notices that the average value for the process is at $74\mathrm{.}5$ mm $,$ not at the target value of $75$ mm $.$ After consulting with the local manufacturing engineer, they decide to re$-$center the process so that it is on target $($i$.$e$.75$ mm $).$ After running with this new mean for some time, they calculate a revised Cpk$.$ What value would they get?

Revised Cpk: $2\mathrm{.}3$

$5\mathrm{.}0$ points possible $[$graded$,$ results hidden$)$

After this change, how many parts would we expect to be out of spec in a lot of $20,000$ parts? Round the nearest part number, i$.$e$.,$ don't report any decimals

You have used $0$ of $3$ attempts

$2\mathrm{.}4$

$5\mathrm{.}0$ points possible $[$graded$,$ results hidden$)$

Now you come along and tell them to use the Quality Loss Function to quantify this problem instead of Cpk$.$ Compare the expected quality loss for the mean being centered on the target value vs$.$ being centered for symmetric limits$.$

$($NB: you can assume that the cost of being above and below the mean is the same and that the calibration constant for $\backslash ($ E$\backslash \{$L$\backslash \}\backslash )$ is $1\backslash \}$

$\backslash (\backslash$mathrm$\{$E$\}\backslash \{\backslash$mathrm$\{$L$\}\backslash \}\backslash )$ if centered at $74\mathrm{.}5$ mm $($spec limits are symmetric about mean$)$:

$2\mathrm{.}5$

$5\mathrm{.}0$ points possible $[$graded$,$ results hidden$)$

$\backslash (\backslash$mathrm$\{$E$\}\backslash \{\backslash$mathrm$\{$L$\}\backslash \}\backslash )$ if centered at $75\mathrm{.}0$ mm $($mean is centered on target value$)$: