Reconsider the data in the previous problem. The response measurements in the two columns were collected on two different days. Fit a new model
\[
y=\theta_{3} x_{2}+\theta_{1} e^{\theta_{2} x_{1}}+\varepsilon
\]
to these data, where \(x_{1}\) is the original regressor from Problem 12.8 and \(x_{2}\) is an indicator variable with \(x_{2}=0\) if the observation was made on day 1 and \(x_{2}=1\) if the observation was made on day 2 . Is there any indication that there is a difference between the two days (use \(\theta_{30}=0\) as the starting value).

Data From Problem 12.8

Consider the following observations:

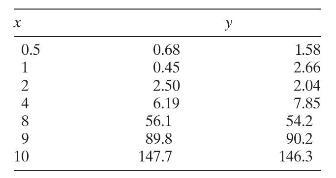
x y 0.5 0.68 1.58 124890 0.45 2.66 2.50 2.04 6.19 7.85 56.1 54.2 89.8 90.2 147.7 146.3