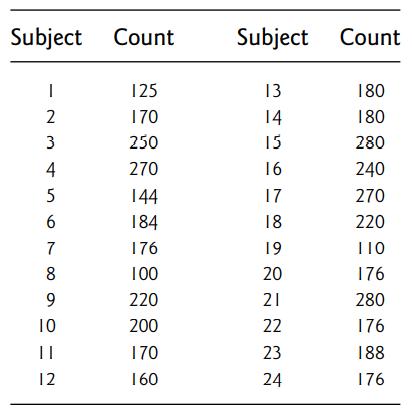
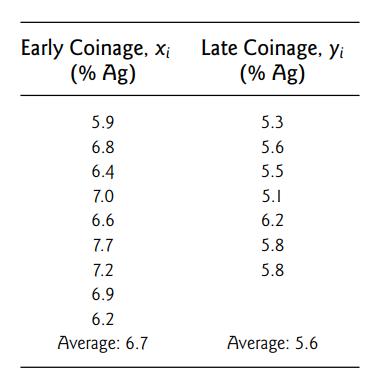
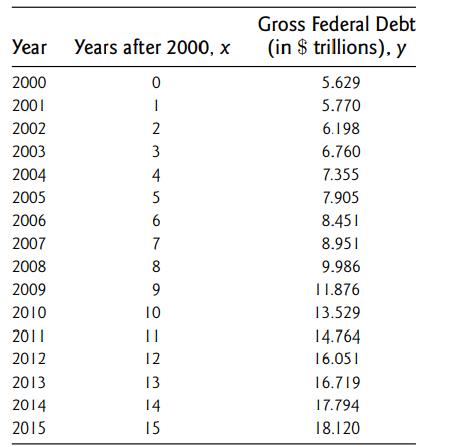
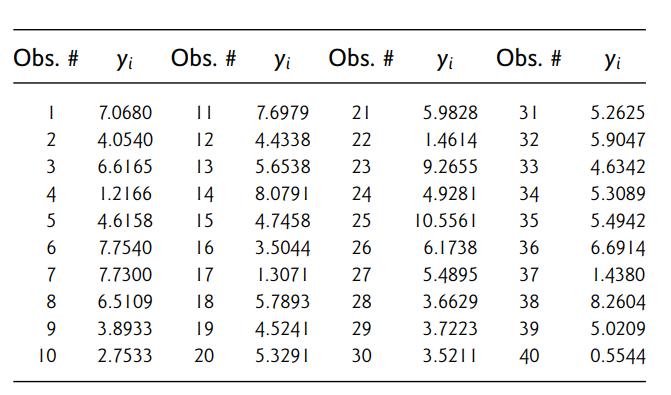
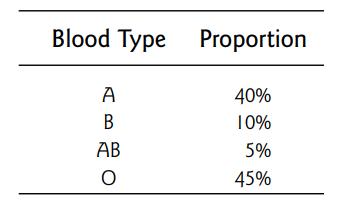
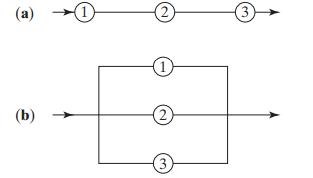
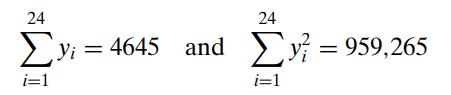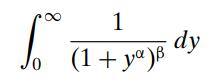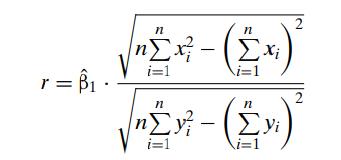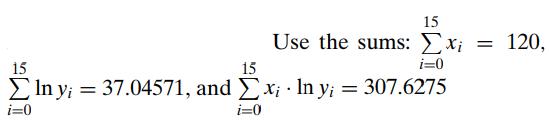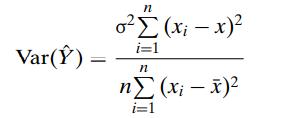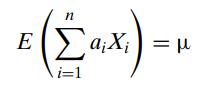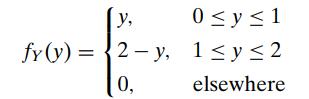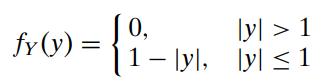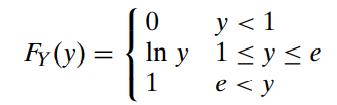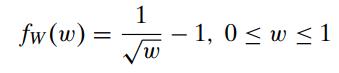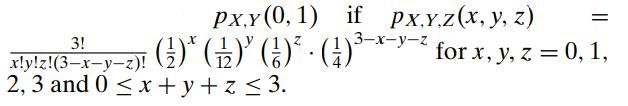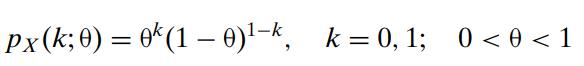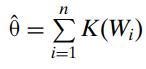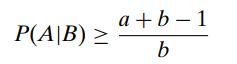Introduction To Mathematical Statistics And Its Applications 6th Edition Richard Larsen, Morris Marx - Solutions

Unlock the full potential of "Introduction To Mathematical Statistics And Its Applications 6th Edition" by Richard Larsen and Morris Marx with our comprehensive solution offerings. Access a complete answers key and solutions manual, providing detailed, step-by-step answers to solved problems and questions. Whether you're seeking chapter solutions or a test bank to enhance your learning, our resources are available for free download. Perfect for students and instructors alike, our textbook solutions and instructor manual deliver the insights needed for mastering statistical concepts effortlessly. Embrace the convenience of online solutions PDF to excel in your studies today!