Consider a second-order system with transfer function

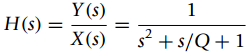
where Y(s) and X(s) are the Laplace transforms of output y(t) and the input x(t) of the system. Q is called the quality factor.

(a) If the feedback gain is unity, determine the feedforward transfer function G(s).

(b) Find the poles of H(s), and plot them expressing the poles as p_1,2 = re^±jφ, where φ is an angle measured with respect to the negative axis, and r is a positive radius, give the values of rand φ. Show that Q = 1/(2cos(φ)).

(c) Consider the cases when Q = 0.5,Q = ˆš2/2 and Q†’ˆž, and determine the corresponding poles. Find the impulse response h(t) for these cases. What happens as Q increases? Explain.

Y (s) H(s) X(s) s2 + s/Q+1