Find the zero-point energy, that is, E = h̄²K²/2m, at k = 0, using (1.2.6) in the limit b → 0 and U₀ → ∞ and U₀b finite but small. To do this, use the approximations for sinKa ≃ Ka and cos Ka ≃ 1 − 1/2 (Ka)², assuming Ka is very small at k = 0.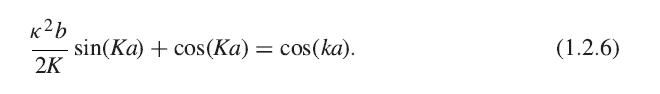

kb 2K sin(Ka) + cos(Ka) = cos (ka). (1.2.6)