Question: EXERCISE 2.1. Consider the differential do = (x + y)dx + xdy. (a) Show that it is an exact differential. (b) Integrate do between the

EXERCISE 2.1. Consider the differential do = (x + y)dx + xdy.

(a) Show that it is an exact differential.

(b) Integrate do between the points A and B in the figure below, along the two different paths, 1 and 2.

(c) Integrate do between points A and B using indefinite integrals.

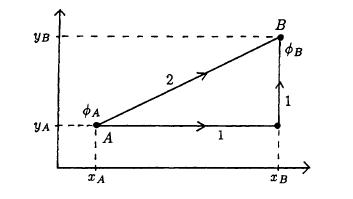
A 2 IA B 1 1 IB

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To solve this exercise lets go stepbystep a Show that it is an exact differential A differential form d o M x y d x N x y d y d o M x y d x N x y d y ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Statistical Techniques in Business Questions!

PLEASE ANSWER ALL QUESTIONS. FOR NUMBERS 9-13, KINDLY SHOW YOUR SOLUTION. THANKS! This is a linear DE. If arranged to its form, what is the integrating factor? * 1 .. : This is an exact differential...

Euler's Method and Modified Euler's Method: Find a numerical solution to the initial value problem (dy / dx) = 2x + y, y(0) = 1 (1) using the Euler method. Use Euler's method to find a numerical...

Answer Key attached for the FRQ. There is no answer key for the third and fourth images. Please Show all work for all problems. Write neatly and show work simply as possible. I am not turning this...

FIND THE SOLUTION AS REQUIRED. USE THE INDICATED METHOD FOR YOUR GUIDE. Nos. 1 -2 - Coefficients Linear in Two Variables 1. (6x-3y+2)dx -(2x-y-1)dy =0 2. (x+y-Ddx+ (2x+2y+1)dy =0 when x = 2, y= -2...

Janagan Kandasamy Assignment Assignment 3 due 10/05/2016 at 11:59pm EDT Z ENRG 213 Fall 2016 1. (1 point) Use the \"mixed partials\" check to see if the following differential equation is exact. If...

E Test: Chapter 5 Test Question list 0 Question 1 0 Question 2 0 Question 3 0 Question 4 0 Question 5 0 Question 6 0 Question 7 0 Question 8 I? Find the anlidelivative utthe given derivative do (X +...

7. [-/1 Points] DETAILS SCALCET8 9.2.TEC.B.001. NVA MY NOTES Concept This module allows you to use Euler's Method to approximate solutions of a variety of differential equations. You can compare the...

2.7. Explicit Solutions to Dierential Equations 109 power (kw) 20 15 10 5 0 08:00 10:00 12:00 14:00 16:00 time 18:00 2.7 Explicit Solutions to Dierential Equations In the very rare case in which an...

1. 3 2 Consider the function f(x) = x - 3x - 9x + 10, x (a) . Find the equation of the straight line passing through the maximum and minimum points of the graph y = f(x). (4) (b) Show that the point...

Section 9.2 Reading Assignment: First-Order Linear Equations Answer Only Exercise 1, 2, and 3 by using a screenshot provided Calculus Pearson textbook. Make sure you read these three questions very...

A telemarketer calls people and tries to sell them a subscription to a daily newspaper. On 20% of her calls, there is no answer or the line is busy. She sells subscriptions to 5% of the remaining...

Saturated water vapor at 200 kPa is in a constant pressure piston cylinder. At this state the piston is 0.1 m from the cylinder bottom. How much is this distance and the temperature if the water is...

What is the payback period of Project X ? 2 . 2 5 years 2 . 3 8 years 2 . 4 9 years 2 . 5 4 years 2 . 8 9 years

XYZ Corporation plans to acquire a building (with a useful life of 10 years) by issuing a $5,000,000, 10-year, 3 percent note to the former owner of the building. XYZ will value the building and the...

Explain the difference between a sample and a population.

Explain the difference between qualitative and quantitative variables. Give an example of qualitative and quantitative variables.

Slate is a daily magazine on the Web. Its business activities can be described by a number of variables. What is the level of measurement for each of the following variables? a. The number of hits on...

Cycle Wholesaling sold merchandise on account, with terms n/60, to Sarah's Cycles on February 1 for $750 (cost of goods sold of $480). On February 9, Sarah's Cycles returned to Cycle Wholesaling...

Current Attempt in Progress Monty Corporation produces snowboards. The following unit cost information is available: direct materials $10, direct labor $9, variable manufacturing overhead $8, fixed...

The Dairy Company had not credit sales of $870,000 for the year Cash sales for the year were $1,130,000 receivables at the beginning of the year were $42,000 and at the end of the year they had...