For the probability distribution in Exercise 14, find the sampling distribution of the sample mean for all samples of size \(n=2\). (Hint: The sample means will be the same as given in Figure 3.7, but the probabilities will be different because each of the outcomes of the random variable \(X\) are not equally likely as they are in Table 3.12. What this means is that the probability of drawing a \(\{1,1\}\) to give a sample mean of 1 would be \((0.20)(0.20)=0.04\). And the probability of drawing a \(\{1,2\}\) or a \(\{2,1\}\) to give a sample mean of 1.5 would be \((0.20)(0.27)+(0.27)(0.20)=0.108\), etc.).

Figure 3.7

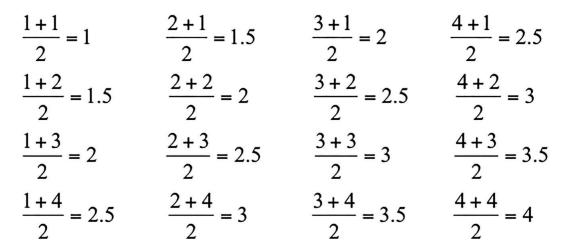
Table 3.12

1+1 2 1 2+1=1.5 2 3+1-24+1=-2.5 2 1+2 2+2 3+2 4+2 = 1.5 = 2 2 1+3 = 2 2 2+3 -2.5 2 = = 2.5 = 3 2 3+3-3 4+3 = = 3.5 2 1+4 2 = 2 2 2 2+4 3+4 4+4 2.5 = 3 = 3.5 = 4 2 2 2