Question: Let X be a random variable with cdf F(x) and let T (F) be a functional. We say that T (F) is a scale functional

Let X be a random variable with cdf F(x) and let T (F) be a functional. We say that T (F) is a scale functional if it satisfies the three properties

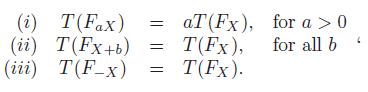
3 (i) T(Fax) (ii) T(Fx+b) (iii) T(F_x) = aT (Fx), T(Fx), T(Fx).

Show that the following functionals are scale functionals.
(a) The standard deviation, T (FX) = (Var(X))^1/2.
(b) The interquartile range, T (FX) = F⁻¹_X (3/4) − F⁻¹_X (1/4).

3 (i) T(Fax) (ii) T(Fx+b) (iii) T(F_x) = aT (Fx), T(Fx), T(Fx). for a > 0 for all b

Step by Step Solution

★★★★★

3.42 Rating (161 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a The standard deviation is a scale functional because by the definitio... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Statistical Techniques in Business Questions!

Let X be a random variable with mean and variance 2, and let X1, X2, , Xn be a random sample of size n from X. Show that the statistic V = k (Xi+1 Xi)2is an unbiased estimator for 2 for an...

Let X be a random variable with probability distribution find the probability distribution of the random variable Y = X2.

Let X be a random variable with density (a) What value of K will make fX(y) a true density? (b) What is the CDF of X? (c) Find E(2X 1). (d) Find variance (X). (e) Find the approximate value of P{Xbar...

Hi there can anyone please help me with this, would really appreciate it!! 4. Let X be a random variable with cdf F and a strictly unimodal continuous pdf f (i.e. the pdf only has 1 mode or 1 global...

Need help please in this homework Chapter 3 Quiz Started: Apr 28 at 9:31am Quiz Instructions Sections 2-9 D Question 1 1 pts Let X be a random variable with cdf 0, x 30) (round off to second decimal...

Set Student Name: 1. Describe the relationship between two variables that have a correlation coefficient value: a. Near -1 b. Near 0 c. Near 1 2. Data was collected where a weightlifter was asked to...

Instuctor's Annotated Edition TENTH EDITION Understandable Statistics Concepts and Methods Charles Henry Brase Regis University Corrinne Pellillo Brase Arapahoe Community College Australia Brazil...

Consider the Markov Chain, Xn, on the states i = 0, 1, 2, . . . with transition matrix given by pi,i1 = p i = 1, 2, . . . pi,i+1 = 1 p i = 0, 1, . . . p0,0 = p where 0

lup ] (d) Show how a generating (or "mother") wavelet (x) can spawn a family of "daughter" wavelets jk(x) by simple shifting and scaling operations, and explain the advantages of representing...

answer the question clearly You are building a flight-control system for which a convincing safety case must be made. Would you assign the tasks of safety requirements engineering, test case...

Multiple choice questions. 1. A company that reproduces fine works of art, such as the Mona Lisa, would most likely use what kind of production process? a. Hybrid b. Conversion c. Job d. Process 2. A...

A point charge 100pC is located at (4, 1, 3) while the x-axis carries charge 2nC/m. If the plane z = 3 also carries charge 5 nC/m2, find E at (1, 1, 1).

# Install Essential Libraries ! pip install ultralytics import numpy as np # linear algebra import pandas as pd # data processing, CSV file I / O ( e . g . pd . read _ csv ) # Input data files are...

Neumann has been likened to a motivational speaker such as Tony Robbins. Why are effective leaders good motivators?

Show that for any set of points (xi , Yi), i = 1, 2, . . . , n. (Y - Y) ! i-1

Based on the data in Question 11.2.1, the relationship between y, the ambient temperature, and x, the frequency of a crickets chirping, is given by y = 25.2 + 3.29x, where s =3.83. At the = 0.01...

Suppose an experimenter intends to do a regression analysis by taking a total of 2n data points, where the xis are restricted to the interval [0, 5]. If the xy-relationship is assumed to be linear...

New Gadgets, Inc., currently pays no dividend but is expected to pay its first annual dividend of $5.00 per share exactly 9 years from today. After that, the dividends are expected to grow at 3.7...

Larry Davis borrows $88,000 at 12 percent interest toward the purchase of a home. His mortgage is for 30 years. Use Appendix D for an approximate answer, but calculate your final answer using the...

19. Ramblin Wreck is a firm specializing in engineering components. The firm is publicly traded and is considering the following project: The project will last 5.00 years with an annual cash flow of...