Mean and standard deviation for a binary random variable The previous exercise gave the formula for the standard deviation of a discrete random variable X. Let’s look at a simple case. Suppose X is a binary random variable where X = 1 with probability p and X = 0 with probability 11 - p2.

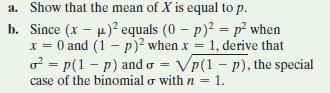
a. Show that the mean of X is equal to p. b. Since (x -) equals (0 - p) = p when x = 0 and (1 - p)2 when x = 1, derive that = p(1 - p) and = p(1 - p), the special case of the binomial or with n = 1.