Normal linear regression (unknown , ). Consider a normal linear regression model for yi , i = 1, . . . , n on xi

Normal linear regression (unknown β, Σ). Consider a normal linear regression model for yi

, i = 1, . . . , n on xi j, j = 1, . . . , k, with a proper multivariate normal prior on β and three alternative priors on the covariance matrix. Let y = (y1, . . . , yn)

0 be an n × 1 vector of responses, X an n × k design matrix

(i.e., a matrix with xi j in the ith row and jth column). Let β = (β1, . . . , βk) be a vector of regression coefficients. We assume

a. Assume that Σ is known. Let Vβ = (X 0Σ
−1X)
−1 , and βˆ = VβX 0Σ
−1 y. Show that h(β | Σ, y) = N(m, V), with

with the last term simplifying to V −1 β
βˆ = X 0Σ
−1 y.

b. We now extend the model by assuming an unknown – but diagonal –
covariance matrix

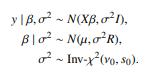
Find h(τ | y) for τ = 1/σ2 and h(β | σ
2 , y) for fixed R, ν0, s0.

c. Replace the prior on β by β ∼ N(µ, T). Find h(τ | β, y).
Note: Together with h(β | σ
2 , y) from question (b), this allows us to define an algorithm that alternately simulates from these two complete conditional posterior distributions. The algorithm is known as the Gibbs sampler and will be discussed at length in Chapter 6. See also Problem 6.11

. . ~ (. ) B-N(T).