Refer to Exercise 26.

a. Generate 10,000 bootstrap samples from the data in Exercise 26. Find the bootstrap sample mean percentiles that are used to compute a \(99 \%\) confidence interval.

b. Compute a \(99 \%\) bootstrap confidence interval for the mean compressive strength, using method 1 as described on page 395.

c. Compute a \(99 \%\) bootstrap confidence interval for the mean compressive strength, using method 2 as described on page 395.

Data From Exercise 26:

A sample of seven concrete blocks had their crushing strength measured in \(\mathrm{MPa}\). The results were 

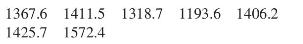
Ten thousand bootstrap samples were generated from these data, and the bootstrap sample means were arranged in order. Refer to the smallest mean as \(Y_{1}\), the second smallest as \(Y_{2}\), and so on, with the largest being \(Y_{10,000}\). Assume that \(Y_{50}=1283.4, Y_{51}=1283.4\), \(Y_{100}=1291.5, Y_{101}=1291.5, Y_{250}=1305.5, Y_{251}=\) \(1305.5, Y_{500}=1318.5, Y_{501}=1318.5, Y_{9500}=1449.7\), \(Y_{9501}=1449.7, Y_{9750}=1462.1, Y_{9751}=1462.1\), \(Y_{9900}=1476.2, Y_{9901}=1476.2, Y_{9950}=1483.8\), and \(Y_{9951}=1483.8\).

1367.6 1411.5 1318.7 1193.6 1406.2 1425.7 1572.4