For the pediatrician presented in Example 1, find the probability that a randomly selected three-year-old girl is between 35 and 40 inches tall, inclusive. That is, find P(35 ≤ X ≤ 40).

By-Hand Approach Step 1 Draw a normal curve and shade the desired area.

Step 2 Convert the values of x to z-scores using 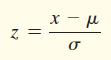Step 3 Use Table V to find the area to the left of each z-score found in Step 2. Use this result to find the area between the z-scores.

Technology Approach

Step 1 Draw a normal curve and shade the desired area.

Step 2 Use a statistical spreadsheet or calculator with advanced statistical features to find the area. The steps for determining the area under any normal curve using the TI-83/84 Plus graphing calculator, Minitab, Excel, and StatCrunch are found in the Technology Step-by-Step.

Data from Example 1

A pediatrician obtains the heights of her three-year-old female patients. The heights are approximately normally distributed, with mean 38.72 inches and standard deviation 3.17 inches. Use the normal model to determine the proportion of the three-year-old females that have a height less than 35 inches

- 2