For testing independence in a contingency table of size r × c, the degrees of freedom (df) for the chi-squared distribution equal df = (r - 1) × (c - 1). They have the following interpretation: Given the row and column marginal totals in an r × c contingency table, the cell counts in a rectangular block of size (r - 1) × (c - 1) determine all the other cell counts. Consider the following table, which cross-classifies political views by whether the subject would ever vote for a female president, based on the 2010 GSS. For this 3 × 2 table, suppose we know the counts in the upper left-hand (3 - 1) × (2 - 1) = 2 × 1 block of the table, as shown.

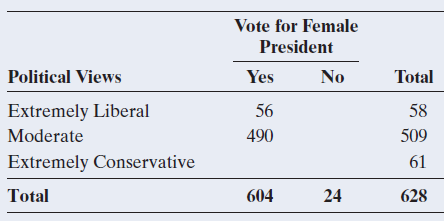
a. Given the cell counts and the row and column totals, fill in the counts that must appear in the blank cells.
b. Now, suppose instead of the preceding table, you are shown the following table, this time only revealing a
2 × 1 block in the lower-right part. Find the counts in the remaining cells.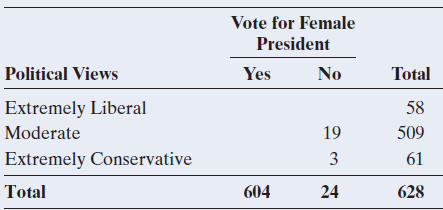

This example serves to show that once the marginal totals are fixed in a contingency table, a block of only (r - 1) × (c - 1) cell counts is free to vary. Once these are given (as in part a or b), the remaining cell counts follow automatically. The value for the degrees of freedom is exactly the number of cells in this block, or df = (r - 1) × (c - 1).

Transcribed Image Text:

Vote for Female President Political Views Yes No Total Extremely Liberal 56 58 490 Moderate 509 Extremely Conservative 61 Total 604 24 628 Vote for Female President Political Views Yes No Total Extremely Liberal 58 Moderate 19 509 Extremely Conservative 3 61 Total 604 24 628