A single twonode beam element is used to model a cantilever beam. The beam is subjected to a transverse load at the tip that is varying harmonically as \(F=\sin t\) and the equation of motion for this system is:

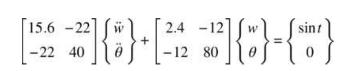
a. Integrate this equation using Newmark method, and plot \(w\) and \(\theta\) for two cycles of the lowest frequency oscillation. Plot \(w\) and \(\theta\) as a function of time. Assume that the initial conditions are: \(\left.\left\{\begin{array}{ll}w & \theta\end{array}\right\}\right|_{t=0}=0\) and \(\left.\left\{\begin{array}{ll}\dot{w} & \dot{\theta}\end{array}\right\}\right|_{t=0}=0\). Use a \(\Delta t\) such that it is one tenth of the period associated with the highest frequency.

b. Using the modal superposition approach, we can decouple the equations of motion to get the following two equations:

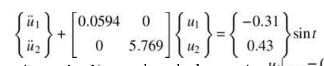
Integrate these two equations using Newmark method, assuming \(\left.u_{i}\right|_{t=0}=0\) and \(\left.\dot{u}_{i}\right|_{t=0}=0\) and compare with the analytically solution.

15.6 -22 -22 40 2.4 W sint 12 80