Consider the springmass system in example 8.4. It is subjected to a timevarying force (in newtons) given by \(F_{2}=100 \sin \omega t\), where \(\omega=0.5 \omega_{\min }\) and \(\omega_{\min }\) is the smallest natural frequency of the system. Assume the system is initially at rest with no initial displacements.

a. Calculate the displacement history \(u_{2}(t)\) in closed form using the mode superposition method.

b. Solve the problem using the central difference method for \(0

c. Solve the above problem (b) using Houbolt method with \(\Delta t \approx 2 \Delta t_{c r}\).

d. Use Newmark method to solve the above problem (b) with \(\Delta t=2 \Delta t_{c r}\).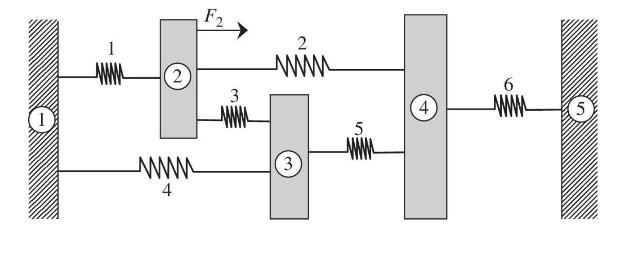

(2) 2 4 3 4 (5)