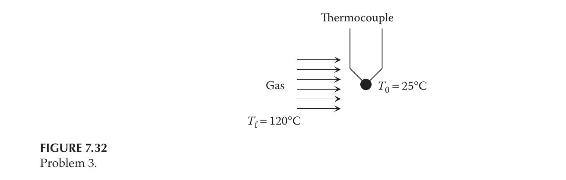
The junction of a thermocouple can be approximated as a sphere with a diameter of \(1 \mathrm{~mm}\). As shown in Figure 7.32, the thermocouple is used to measure the temperature of a gas stream. For the junction, the density is \(ho=8500 \mathrm{~kg} / \mathrm{m}^{3}\), the specific heat capacity is \(c=320 \mathrm{~J} /\left(\mathrm{kg} \cdot{ }^{\circ} \mathrm{C}\right)\), and the thermal conductivity is \(k=40 \mathrm{~W} /\) \(\left(\mathrm{m} \cdot{ }^{\circ} \mathrm{C}\right)\). The temperature of the gas \(T_{\mathrm{f}}\) is \(120^{\circ} \mathrm{C}\) and the initial temperature of the sphere \(T_{0}\) is \(25^{\circ} \mathrm{C}\). The heat transfer coefficient between the gas and the junction is \(h=70 \mathrm{~W} /\left(\mathrm{m}^{2 . \circ} \mathrm{C}\right)\).

a. Determine if the junction's temperature can be considered uniform.

b. Derive the differential equation relating the junction's temperature \(T(t)\) and the gas's temperature \(T_{\mathrm{f}}\).

c. Using the differential equation obtained in Part (b), construct a Simulink block diagram to find out how long it will take the thermocouple to read \(99 \%\) of the initial temperature difference.

Transcribed Image Text:

Gas FIGURE 7.32 Problem 3. T=120C Thermocouple To=25C