Question: The system shown below obeys the differential equation i.e., Input-Output model). [left(m_{1}+m_{2}ight) ddot{x}+left(b_{1}+b_{2}ight) dot{x}+k x=f(t)-m_{2} g,] where (x_{1}=x_{2}=x). (a) Verify that the differential equation is
The system shown below obeys the differential equation i.e., Input-Output model).
\[\left(m_{1}+m_{2}ight) \ddot{x}+\left(b_{1}+b_{2}ight) \dot{x}+k x=f(t)-m_{2} g,\]
where \(x_{1}=x_{2}=x\).
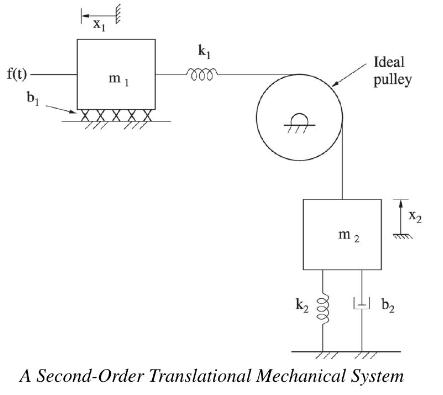
(a) Verify that the differential equation is correct.
(b) Find the expressions for the damping coefficient \(\xi\) and the undamped natural frequency \(\omega_{n}\).
(c) Find the steady-state response when the force is a step unit function.
f(t)- mi b XXXXX k 000 Ideal pulley m2 x2 k b A Second-Order Translational Mechanical System
Step by Step Solution
3.45 Rating (165 Votes )
There are 3 Steps involved in it
a Verification of the differential equation from the free... View full answer

Get step-by-step solutions from verified subject matter experts


