Consider a closed-loop control system with a negative unity feedback and the open-loop transfer function below \((k>0)\). Determine the characteristic equation of the closed-loop system if its root locus has a break-away/break-in point on the real axis in \(-\frac{4}{9}\) and the straight-line asymptotes intersection in \(-\frac{11}{9}\).

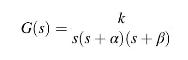
1) \(s^{3}+11 s^{2}+8 s+k\)
2) \(s^{3}+\frac{11}{3} s^{2}+8 s+k\)
3) \(s^{3}+11 s^{2}+\frac{8}{3} s+k\)
4) \(s^{3}+\frac{11}{3} s^{2}+\frac{8}{3} s+k\)

G(s) = k s(s+a)(s+b)