Team Project, Geometric ApplicationsTo increase your skill in dealing with vectors, use vectors to prove the following (see the figures)(a) The diagonals of a parallelogram bisect each other.(b) The line through the midpoints of adjacent sides of a parallelogram bisects one of the diagonals in the ratio 1:3.(c) Obtain (b) from (a).(d) The three medians of a triangle (the segments from a vertex to the midpoint of the opposite side) meet at a single point, which divides the medians in the ratio 2:1.(e) The quadrilateral whose vertices are the midpoints of the sides of an arbitrary quadrilateral is a parallelogram.(f) The four space diagonals of a parallelepiped meet and bisect each other.(g) The sum of the vectors drawn from the center of a regular polygon to its vertices is the zerovectors.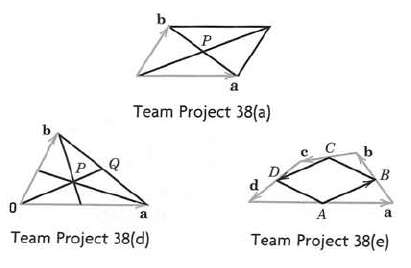

b Team Project 38(a) a a Team Project 38(d) d B A Team Project 38(e) a