The potential energy of a mass m as a function of position is given by U(x) = U₀(a + 1/a), where a = x/a and a is a constant.

(a) Plot U(x) versus x for 0.1a < x < 3a.

(b) Find the value of x = x0 at stable equilibrium.

(c) Write the potential energy U(x) for x = x₀ + ε, where ε is a small displacement from the equilibrium position x0.

(d) Approximate the 1/x term using the binomial expansion with r = ε/x₀ << 1 and discarding all terms of power greater than r².

(e) Compare your result with the potential for a simple harmonic oscillator. Show that the mass will undergo simple harmonic motion for small displacements from equilibrium and determine the frequency of this motion.

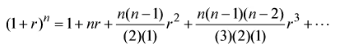
(1+r)" 1+ nr + , 2 , (-)(n 2) ; (2)(1) (- 1), |(1+)" 1+ mr + (3)(2)(1) +...