Two discrete-time systems T1 and T2 are connected in cascade to form a new system T as shown in figure. Prove or disprove the following statements.

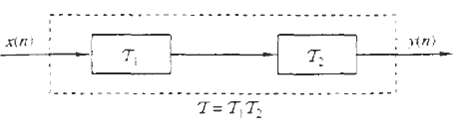
(a) If T1 and T2 are linear, than T is linear (i.e., the cascade connection of two linear system in linear).

(b) If T1 and T2 are time invariant, then T is time invariant.

(c) If T1 and T2 are causal, then T is causal.

(d) If T1 and T2 are linear and time invariant, the same holds for T.

(e) If T1 and T2 are linear and time invariant, then interchanging their order does not change the system T.

(f) As in part (e) except that T1, T2 are now time varying.

(g) If T1 and T2 are nonlinear, then T is nonlinear.

(h) If T1 and T2 are stable, then T is stable.

(i) Show by an example that the inverse of parts (c) and (h) do not hold ingeneral.

T: T= TT