Question: Use integration to determine the moment of inertia of a thin circular hoop of radius R and mass M for rotation about a diameter. Check

Use integration to determine the moment of inertia of a thin circular hoop of radius R and mass M for rotation about a diameter. Check your answer by referring to Table 9-1.

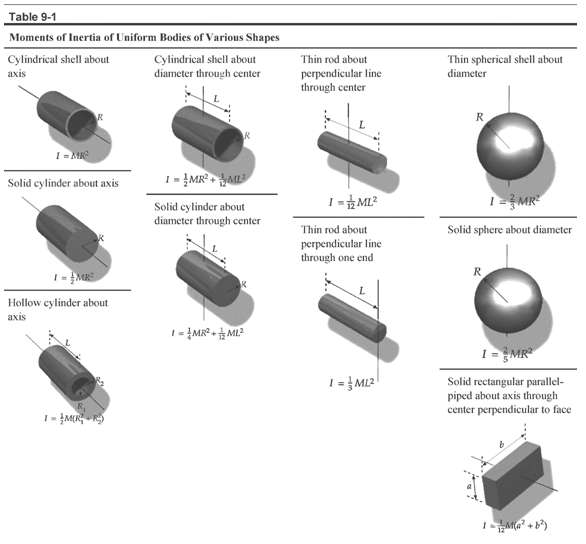
Table 9-1 Moments of Inertia of Uniform Bodies of Various Shapes Cylindrical

Table 9-1 Moments of Inertia of Uniform Bodies of Various Shapes Cylindrical shell about Cylindrical shell about diameter through center Thin rod about Thin spherical shell about perpendicular line through center axis diameter Solid cylinder about axis 1=MR I=ML? Solid cylinder about diameter through center Thin rod about Solid sphere about diameter perpendicular line through one end R. 1- M Hollow cylinder about axis 1= MR 1= MI2 Solid rectangular parallel- piped about axis through center perpendicular to face

Step by Step Solution

★★★★★

3.57 Rating (157 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Here dm R d and dI z 2 dm whe... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (1 attachment)

10-P-M-R-R (158).docx

120 KBs Word File

Students Have Also Explored These Related Mechanics Questions!

A cylinder with radius R and mass M has density that increases linearly with distance r from the cylinder axis, p = ar, where a is a positive constant (a) Calculate the moment of inertia of the...

A thin hoop of radius R and mass M oscillates in its own plane hanging from a single fixed point. Attached to the hoop is a small mass M constrained to move (in a frictionless manner) along the hoop....

Determine the moment of inertia of the cross-sectional area about the xaxis. 10 mm 180 mm 100 mm 10 mm -100 mm- 10 mm

please answer this question with clear physics diagram and using vector sign. 3. A thin circular hoop of radius R = 20 cm and mass M = 5 kg rotates about an axis along a diameter of the hoop at 2000...

W AutoSave Off M25a rotational statics and dynamics 03.16.22 (1) . Saved to this PC v 9 Search (Alt+Q) shemar tulloch ST X File Home Insert Draw Design Layout References Mailings Review View Help...

Mini lab report that includes: 1)Title of the Experiment, 2)Introduction/Purpose. It should be about half of page long and describe what was the purpose of the experiment,which specific physics laws...

1. The moment of inertia of a long rod spun around an axis through one end perpendicular to its length is -2. Why is this moment of inertia greater than it would be if you spun a point mass M at the...

3. Find the net torque on the wheel about the axle through point O perpendicular to the page taking r1=10.0 cm and r2=25.0 cm. Answer -3.55 Nm 10.0 N ry=25.0cm ry=10.0cm 12.0 N. 9.00 N In all the...

Question 1 (1 point) Calculate the moment of inertia | of a hollow sphere of radius 85 cm and mass 39 kg 2 rotating through a central axis. Use units of kg.m , and express your answer with a single...

A bicycle wheel has a diameter of 0.640 m and a mass of 1.80 kg. Assume that the wheel is a hoop with all the mass concentrated on the outside radius. The bicycle is placed on a stationary stand, and...

Analyze Gateway's decisions to change advertising agencies so many times over the past six years. Identify and discuss specific factors that may have led to each decision to change agencies.

Using the data for Problem 9.2 on the student data set, create a time phased budget for the project. Show how much the daily and cumulative costs for the project are just as the monthly and...

If a company issues a $ 1 , 0 0 0 bond with an interest rate of 2 percent and a maturity date of 2 0 4 0 , how much interest does the company pay and for how long? Multiple choice question. $ 2 0 at...

Solve each of the following pairs of simultaneous equations a. y = x + 4 y = |x 2 - 16| b. y = x y = |3x - 2x 2 | c. y = 3x y = |2x 2 - 5|

a. Express 1 + 4x - x 2 in the form a - (x + b) 2 , where a and b are constants to be found. f(x) = 1 + 4x - x 2 for x 2 b. Find the coordinates of the turning point of the function f(x), stating...

Find the range for each of these functions. a. f(X) = x - 5, -2 x 7 b. f(x) = 3x + 2, 0 x 5 c. f(x) = 7 - 2x, - 1 x 4 d. f(x) = x 2 , - 3 x 3 e. f(x) = 2 x , - 3 x 3 f. f(x) = 1/x, 1 x 5

Solve the following simultaneous equations. xy = 2 x + y = 3

Dexter Manufacturing reports depreciation expense for certain machinery purchased this year using an accelerated method for income tax purposes and the straight-line basis for financial reporting...

Calculate P(0), P(1), P(2), P(3), P(4), P(5), P(6), and P(>6) for a Poisson variable with a mean of 1.2. Using this probability distribution determine the mean and variance.

When a person stands on tiptoe (a strenuous position), the position of the foot is as shown in Figure P12.50a. The gravitational force on the body Fg is supported by the force n exerted by the floor...

A person bending forward to lift a load with his back (Fig P12.51a) rather than with his knees can be injured by large forces exerted on the muscles and vertebrae, the spine pivots mainly at the...

A uniform rod of weight Fg and length L is supported at its ends by a frictionless trough as shown in Figure P12.52. (a) Show that the center of gravity of the rod must be vertically over point O...

Miss Jones is a wheat farmer, and she is expecting to produce 5000 bushels in 3 months, i.e:, July. She would like to hedge the price of wheat using futures (future contracts). The current wheat...

Japanese investors purchased from Walt Disney Productions projected yen royalties. The 20-year stream of royalties is for Tokyo Disneyland. The present value of that stream of royalties, discounted...

QUESTION 26 1 points Which of the following factors are related to an ADR? Factor-1: An ADR is a certificate that represents ownership of a foreign stock. An ADR is typically created by a U.S. bank...