Question: (a) A basic building block is shown in Fig. 407. Find the corresponding temperature and complex potential in the upper half-plane. (b) Conformal mapping, what

(a) A basic building block is shown in Fig. 407. Find the corresponding temperature and complex potential in the upper half-plane.

(b) Conformal mapping, what temperature in the first quadrant of the z-plane is obtained from (a) by the mapping w = a + z2 and what are the transformed boundary conditions?

(c) Superposition, find the temperature T* and the complex potential F* in the upper half-plane satisfying the boundary condition in Fig. 408.

(d) Semi-infinite strip, applying w = cosh z to(c), obtain the solution of the boundary value problem in Fig.409.

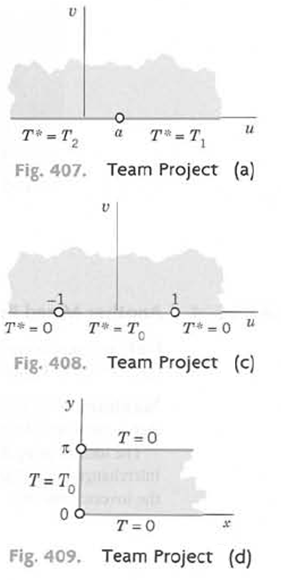
D T* = T T = T Fig. 407. Team Project (a)

D T* = T T = T Fig. 407. Team Project (a) y TO T-0 T* = To T=0 Fig. 408. Team Project (c) T = T V 00 a U T=0 u T=0 Fig. 409. Team Project (d)

Step by Step Solution

★★★★★

3.28 Rating (163 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Team Project a Arg z or Arg w is a basic building block when we have jumps in the boundary values To ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (1 attachment)

1-M-C-A-P-T (10).docx

120 KBs Word File

Students Have Also Explored These Related Complex Analysis Questions!

The block diagram of a digital control system is shown in Fig. The sampling period is ?t 1 min.(a) Design the digital controller Gc(z) so that the closed-loop system exhibits a first-order response...

A thin circular-arc airfoil is shown in Fig. P9.156. The leading edge is parallel to the free stream. Using linearized (small turning- angle) supersonic-flow theory, derive a formula for the lift and...

A five-bus power system is shown in Fig. 9.14. The line, bus, transformer, and capacitor data are given in Tables 9.6, 9.7, 9.8, and 9.9, respectively. Use the Gauss-Seidel method to find the bus...

DONT POST THE RANDOM CIRCUIT SOLUTION. I WILL DOWNVOTE. PLEASE ANSWER PROMT (a) A basic building block is shown in Figure 1. Find the corresponding temperature and complex potential in the upper...

Summarize this for me. Someone who understand the HEA and MEA perfectly and also the summary should be 2 or over 2 pages. Someone who understands this perfectly A scrap-tolerant alloying concept...

A creative engineer suggests structuring the TLB so that not all the bits of the presented address need match to result in a hit. Suggest how this might be achieved, and what might be the costs and...

Portray in words what transforms you would have to make to your execution to some degree (a) to accomplish this and remark on the benefits and detriments of this thought.You are approached to compose...

Prolog You are approached to compose a Prolog program to work with twofold trees. Your code shouldn't depend on any library predicates and you ought to expect that the mediator is running without...

PART I"Basic Building Block" Excel Model Creation (Groups of up to 3individuals for Part I) Reference any all CCIM/G-M modules/chapters in course textbook or the library for any required supporting...

Fruit1 -- 50 pts Write a program called "Fruit1" that reads a sequence of fruit purchases from file. Each purchase consists of the name of a fruit, the quantity purchased, and the unit cost. Store...

Hg undergoes electron capture. Write a balanced nuclear equation for this process. 80 201 80 Hg+e TI 202 81 O 201 80 201 Hg+e Au 81 201 Hg +e 80 201 81 O 201 80 202 Hg+e 79 Au O 201 80 201 Hg+je- 79

Explain the differences between USP and brand image creative styles, and indicate the specific conditions under which each is more likely to be used. Provide one illustration of each creative style,...

E4-30B Compute activity cost allocation rates (Learning Objective 2) TECH manufactures electronic appliance products based on customer orders and uses an activity-based costing system. Wages and...

Calculate the Avf, Rif, R'of for the circuit shown in figure 2. Both transistors are identical and their parameters, h-1100 2, and he-50. The values of the circuit parameters are: R=1KN, R=100KN,...

Explain the dynamic tree problem and what steps been taken to mitigate the issue ?

A stirred-tank fermentation reactor has height 2 m, diameter 1.5 m, and is filled with a fermen- tation broth that can be assumed to have the physical properties of water. The fermenter must be must...

Write the Quotient (Keq) of the reaction for high ionic strength water (activity coefficients needed). Label the terms of the equation. how to calculate the activity coefficients. 2KAlSi 3 O 8 (s) +...

Refer back to the Series EE savings bonds wediscussed at the very beginning of the chapter. a. Assuming you purchased a $50 face value bond, what is the exact rate of returnyou would earn if you held...

Verify that y is a solution of the ODE. (b) Determine from y the particular solution of the IVP. (c) Graph the solution of the IVP. y' tan x = 2y - 8, y = c sin 2 x + 4, y(1/2) = 0

Find the general solution. If an initial condition is given, find also the corresponding particular solution and graph or sketch it. (Show the details of your work.) y' cos x + (3y - 1) sec x = 0,...

Sketch or graph some of the given curves. Guess what their OTs may look like. Find these OTs. x 2 + (y - c) 2 = c 2

Graph a direction field (by a CAS or by hand) and sketch some solution curves. Solve the ODE exactly and compare. y' = 1 - y 2

Test for exactness. If exact, solve. If not, use an integrating factor as given or obtained by inspection or by the theorems in the text. Also, if an initial condition is given, find the...

Houston Inc. is considering a project which involves building a new refrigerated warehouse which will cost $7,000,000 at t = 0 and which is expected to have operating cash flows of $500,000 at the...