In this problem you will derive Equation 35-28 for the resolving power of a diffraction grating containing N slits separated by a distance d. To do this you will calculate the angular separation between the maximum and minimum for some wavelength λ and set it equal to the angular separation of the mth-order maximum for two nearby wavelengths.

(a) Show that the phase difference ф between the light from two adjacent slits is given by

(b) Differentiate this expression to show that a small change in angle dθ results in a change in phase of dф given by

(c) For N slits, the angular separation between an interference maximum and interference minimum corresponds to a phase change of dф = 2π/N. Use this to show that the angular separation dθ between the maximum and minimum for some wavelength λ is given by

(d) The angle of the mth-order interference maximum for wavelength λ is given by Equation 35-27. Compute the differential of each side of this equation to show that angular separation of the mth-order maximum for two nearly equal wavelengths differing by dλ is given by

(e) According to Rayleigh’s criterion, two wavelengths will be resolved in the mth order if the angular separation of the wavelengths given by Equation 35-31 equals the angular separation of the interference maximum and interference minimum given by Equation 35-30. Use this to derive Equation 35-28 for the resolving power of a grating.

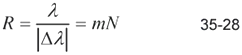
2d -sin 0